I understand the first step in the Cirac-Zoller controlled-phase gate; about how to move the state from the electronic state to the vibrational mode state. However, I am unable to understand how a $2\pi$ pulse gives the -1 sign to the state and how it is applied conditioned on the vibrational mode. Any help is appreciated.
1 Answers
CNOT in ion traps is not implemented in one go. It is decomposed in terms of SWAP gate. The general decomposition they use is:
\begin{equation} \operatorname{CNOT}_{jk}=H_k \operatorname{SWAP}^{-1}_k C_j(Z) \operatorname{SWAP}_kH_k \end{equation} where $j,k$ are the labels for the control and target ion (qubit) respectively, in the array. $H$ is Hadamard gate and $C(Z)$ is the control-Z operation.
Hadamard is just rotations, so we can ignore that for a while and focus on the middle three gates, they are the three crucial steps of the algorithm of Cirac-Zoller implementation in the right order.
The circuit is as shown (Source: Nielsen and Chuang, pg.323)
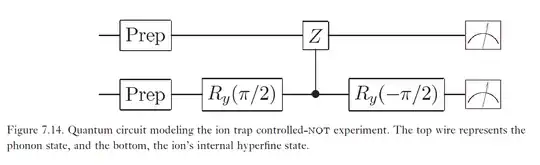
The Control-Z is what the $2\pi$ pulse is in the second step.
If you follow this scheme of Nielsen and Chuang (sec-7.6.4), the $2\pi$ pulse implements this operation as follows:
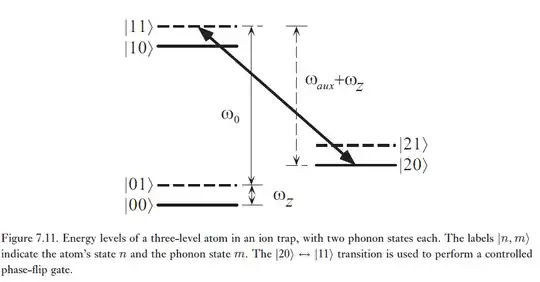
We need to switch $|01\rangle \leftrightarrow |10\rangle$ for the control-Z. This is done as follows. We need a way to swap qubits between the atom’s internal spin state and the phonon state (little perturbation over the spin states). This can be done by tuning a laser to the frequency $\omega_0-\omega_z$, and arranging for the phase (which can always be done by the laser) to be such that we perform the rotation $R_y(\pi)$ on the subspace spanned by $|01\rangle$ and $|10\rangle$, which is just the unitary transform
\begin{equation} C_{SWAP}=|00\rangle \langle 00|+|01\rangle \langle 10|-|10\rangle \langle 01|+|11\rangle \langle 11| \end{equation} on the $|00\rangle, |01\rangle, |10\rangle, |11\rangle$ space. If the initial state is $a|00\rangle + b|10\rangle$ (that is, the phonon is initially $|0\rangle$), then the state after the swap is $a|00\rangle + b|01\rangle$, so this accomplishes the desired swap operation, which is the second step in Cirac-Zoller. Note here that $2\pi$ pulse is just the $R_y(\pi)$ here which is equivalent by just a convention.
The frequency notation is explained in the last image.
I would suggest to read thoroughly the section 7.6 of Nielsen and Chuang to make a complete understanding.
- 1,795
- 9
- 22