Proof of optimality for CHSH game classical strategy

Question

I'm aware that the optimality of the quantum strategy for the CHSH game is given by Tsirelson's bound, but presentations all skip over the (admittedly much less interesting) proof of the classical strategy's optimality.

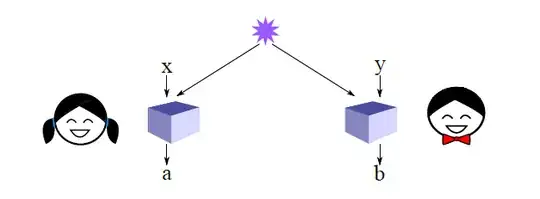
In the CHSH game, we have two players: Alice and Bob. They are separately given independent random bits $X$ and $Y$ as input, and without communication must output bits of their own ($A$ and $B$) with the goal of making true the logical formula $X \cdot Y = A \oplus B$. The claimed optimal classical strategy is for Alice and Bob to both always output $0$, which results in a win 75% of the time:

$\begin{array}{|c|c|c|c|c|c|} \hline X & Y & A & B & X \cdot Y & A \oplus B \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 0 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 0 & 0 & 1 & 0 \\ \hline \end{array}$

The quantum strategy (which I go over here) results in a win ~85% of the time. You can use this in a proof of the insufficiency of local hidden variables to explain entanglement as follows:

1. Assume qbits decide at time of entanglement how they will collapse (rather than at time of measurement); this means they must carry with them some information (the local hidden variable), and this information can be written as a string of bits.
2. Since the information is sufficient to completely describe the way in which the entangled qbits collapse, Alice and Bob could, if given access to that same string of classical bits, simulate the behavior of a shared pair of entangled qbits.
3. If Alice and Bob could simulate the behavior of a shared pair of entangled qbits, they could implement the quantum strategy with local classical methods using the pre-shared string of classical bits. Thus, there must exist some classical strategy giving an 85% success rate with some string of bits as input.
4. However, there exists no string of bits which enables a classical strategy with success rate above 75%.
5. By contradiction, the behavior of entangled particles is not reducible to a string of bits (local hidden variable) and thus the entangled particles must instantaneously affect one another at time of measurement.

I'm interested in the proof of (4). I imagine this proof takes the form of a noncommunicative pair of Turing machines which take as input independent random bits $X$ and $Y$ plus an arbitrary shared bitstring, which then win the CHSH game with probability greater than 75%; presumably this results in some contradiction demonstrating the nonexistence of such TMs. So what is this proof?

Secondarily, which papers have presented a proof of the classical strategy's optimality?

Bonus question: in (1), we claim that the local hidden variable can be written as a string of bits; is there a simple reason why this is the case?

Answer 1

I would argue that this is the critical issue to understand for Bell inequalities. Finding a violation of a Bell inequality tells you that the system is not classical (note: it does not prove that it is quantum), so you need to understand what the classical thing is that the world is not.

Let's state the CHSH random variable that we're interested in: $$ S=A_1B_1+A_1B_2+A_2B_1-A_2B_2, $$ where each of $A_1,A_2,B_1,B_2$ are random variables with $\pm1$ values. The key assumption for the classical strategy is that for every run of the experiment, all four variables have a fixed value (even though we only ever find out two of the values). Hidden variables are essentially irrelevant here - they let two distant parties coordinate what those fixed values will be without having to communicate in the moment, but cannot change this basic assumption.

What are the consequences of this? Rewrite $S$ as $$ S=A_1(B_1+B_2)+A_2(B_1-B_2). $$ Now, if $B_1\in\{\pm1\}$ and $B_2\in\{\pm1\}$, then either $B_1=B_2$, in which case $B_1-B_2=0$ and $B_1+B_2=\pm 2$, or $B_1=-B_2$, such that $B_1+B_2=0$ and $B_1-B_2=\pm 2$. In either case, $S=\pm 2$. Finally, if, in every run of the experiment, $S=\pm 2$, then the average value $|\langle S\rangle|\leq 2$.

So, what you learn from violation of a Bell inequality is that, each time the experiment is run, not all of the possible answers were determined. Classically, this is possible with the locality loophole -- if both questions are known, then a winning answer can be deterministically decided without having to specify all the other possible outcomes. Otherwise, there's some inherent randomness in play at picking the answers.

As for where you might find proofs in the literature, why not follow up on the references in the wikipedia article? As I say, the classical bound is the central element, so it must be in the original papers.

Bonus question: in (1), we claim that the local hidden variable can be written as a string of bits; is there a simple reason why this is the case?

Any information can be written as a string of bits.

Answer 2

One way to go about proving this is to characterise the set of all possible strategies that Alice & Bob can adopt. By "strategy" here I mean a possible relation between inputs and outputs, encoded in the set of four binary numbers $A_0,A_1,B_0,B_1$.

It is worth noting that it doesn't matter whether we are considering deterministic or probabilistic protocols here. The difference between these two approaches is in the way the steps of the protocol proceed, but if one considers only input and output of the protocol, without caring about how the output is actually obtained, then characterising the set of all possible input-output relations and showing that none of these combinations gives a winning probability greater than $75\%$ is enough. In other words, using a probabilistic approach does not expand the number of possible outcomes/strategies, but only provide a different way to get to them. Because we are only interested in the final winning probability, and therefore in the overall strategy, we don't need to take into account separately deterministic and probabilistic case.

Note that, given a strategy $\mathcal S\equiv\{A_0,A_1,B_0,B_1\}$, we can write the number of input combinations for which this strategy gives the wrong result as $$P_{\mathcal S}\equiv A_0\oplus B_0 + A_0\oplus B_1 + A_1\oplus B_0 + (1-A_1\oplus B_1),\tag1$$ where $a\oplus b$ denotes addition modulo 2.

Our problem is to find the strategy $\mathcal S$ that minimises $P_{\mathcal S}$.

Now, there are several ways to do this.

Brute force

The simplest way, if the least elegant, is to compute the value of $P_{\mathcal S}$ for all the possible strategies $\mathcal S$. There are 16 of these, so this isn't too bad. With a few lines of code you can obtain the following table $$ \left( \begin{array}{ccccc} A_0 & A_1 & B_0 & B_1 & P_{\mathcal S} \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1 & 3 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 3 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 3 \\ 1 & 0 & 0 & 0 & 3 \\ 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 3 \\ 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 3 \\ 1 & 1 & 0 & 1 & 3 \\ 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ \end{array} \right) $$ which confirms that indeed all possible strategies lead to the game being lost for at least one input combination (that is, in your words, to a success probability not greater than $75\%$).

But now, of course, this is not a very satisfying way to solve the problem (for me at least). It would be much nicer to have a way to prove optimality without having to check all possibilities. The main hurdle to overcome is that Eq. (1) contains both modular sums and regular sums, which makes manipulation a bit awkward, as we cannot write something like $A_0\oplus B_0+A_0\oplus B_1=A_0(B_0\oplus B_1)$.

I can see two ways around this, the second of which also sheds light to the similarities between this formalism and the regular proof of the CHSH inequalities.

First method

A way around this problem is to notice that we can express modular sums using regular sums and products, as following $$A\oplus B=(1-A)B+A(1-B)=A+B-2AB.$$ Simple algebraic manipulation thus allows us to write $$A_0\oplus B_0+A_0\oplus B_1=2A_0(1-(B_0+B_1))+(B_0+B_1),\\ A_1\oplus B_0+(1-A_1\oplus B_1)=1+(2A_1-1)(B_1-B_0),$$ and finally $$P_{\mathcal S}=1+2\{B_0+A_0[1-(B_0+B_1)]+A_1(B_1-B_0)\}.$$

You can now verify that if $B_0=B_1$ then $P_{\mathcal S}=1+2A_0\oplus B_0$, while if $B_0+B_1=1$ then $P_{\mathcal S}=1+2A_1\oplus B_0$.

Equivalently, one can verify that $P_{\mathcal S}$ can also be written as $$P_{\mathcal S}=(1-2B_0)(B_1-B_0)[1+2A_1\oplus B_0] + [1-(B_0+B_1)](1-2B_0)[1+2A_0\oplus B_0]+ B_0(1-B_0)(...),$$ where the last term is always zero as $B_0\in\{0,1\}$. Note that this is just a way to express algebraically what happens in the two cases $B_0=B_1$ and $B_0=-B_1$, as $(1-2B_0)(B_1-B_0)=1$ iff $B_0=-B_1$, and $(1-2B_0)(1-B_0-B_1)=1$ iff $B_0=B_1$.

Second method

This involves showing that this formalism is equivalent to the one commonly used in the context of deriving the CHSH inequalities.

Denote with $\tilde A_x\equiv 1-2A_x$ the number obtained by replacing $0,1$ in $A_x$ with $+1,-1$, respectively, and similarly for $\tilde B_y$. For example, $A_x=0$ gives $\tilde A_x=+1$. Note that, under this mapping, we have the identities $$A_x\oplus B_y=(1-\tilde A_x\tilde B_y)/2.$$ We can then write

$$P_{\mathcal S}=\frac{1}{2}\left[4-\tilde A_0\tilde B_0-\tilde A_0\tilde B_1-\tilde A_1\tilde B_0+\tilde A_1\tilde B_1\right] =2 - S/2,$$ where we defined $$S\equiv \tilde A_0\tilde B_0+\tilde A_0\tilde B_1+\tilde A_1\tilde B_0-\tilde A_1\tilde B_1,$$ which you might recognise as equivalent to the operator $\hat S$ used when discussing the CHSH inequalities.

Standard arguments now give you $S=\pm 2$, and thus $\lvert S\rvert\le 2$, and finally $P_{\mathcal S}\ge1$ (or more precisely $P_{\mathcal S}\in\{1,3\}$).

Answer 3

In the CHSH game we have 2 players Alice and Bob. Can we proof in the form of a noncommunication pair of TMs which takes as input independant random bits x and y plus an arbitrary shared bitstring, that ALice and Bob win the CHSH game with probability greater than 75%.

We ask Alice and Bob questions x and y with probability p(xy) they give answers a and b. The rules of the game are denoted using $V(a,b|x,y)$wich takes the value "1" if a and b are the winning answers. The probability that Alice and Bob win the game is maximized over all possible strategies $ P_{win} = max_{strategy} \sum_{x,y} p(x,y) | \sum_{a,b} V(a,b|x,y) p(a,b|x,y). $ Where $p(a,b|x,y) $ is the probability that Alice and Bob produce answers a and b given x and y.

In terms of probabilities there is an distinction between a classical deterministic prob and a classical shared ramdoness probability. A deterministic classical stratey is given by the functions $f_{A}(x) = a$ and $f_{B}(y) = b $ that take the questions x and y.

If we have shared randomness another string r is used with a sharing probability $p(r)$. Classicaly Alice and Bob can only apply functions $a = f_{A}(x,r)$ and $b = f_{b}(y,r)$ This gives $ p(a,b|x,y) = \sum_{x,y}^{} (p(r)) p(a,b|x,y,r) $ In this case the pobability of winning the game is

$ P_{win} = max_{strategy} \sum_{x,y} p(x,y) \sum_{a,b} V(a,b|x,y)\sum_{r}p(r)p(a,b|x,y,r)$. In this case of shared randomnes we have an extra term with the string r. Alice and Bob can fix the best possible r given a deterministic strategy for a and b. So it is possible to run an algorithm on a Turing machine using a string r according to the test setup in the picture. Problem how do we find the best possible string r?

Another way to look at it is to say that the string r as a shared randomness is referred to as a hidden variabele in physics. So the Hidden Variabele Theory is equivalent to using a string r in a turing machine. Therefore we might just as well make use of a proof of the CHSH inequality. Furthermore we can compare an arbitrary HVT (dashed line ) and QM results for a photonic experiment.

A compact proof of the CHSH inequality based on a hidden variabele can be found in the article Entangled photons, nonlocality and Bell inequalities in the undergraduate laboratory.