How can you measure qubits in QuTiP?
As far as I have seen you can define a Hamiltonian and let it evolve in time. It is also possible to define a quantum circuit, however, measuring and running it is not possible.
Does anyone know how to do this?
A simple circuit could be
H q[0]
CNOT q[0],q[1]
Measure q[0], q[1]
QuTiP is not really meant for this I think. As said on the home page :
QuTiP is open-source software for simulating the dynamics of open quantum systems.
Simulating dynamics of open quantum systems by definition means you are interested in the quantum state as a result of your algorithm.
I tried looking at the Notebook examples provided in this Github but could not find measurement examples somewhere. You have a possibility to get expectation values though (see this notebook).
If you really want to simulate measurement, that's how I would do it.
A function that finds probability amplitude associated to each eigenstate.
import numpy as np
import itertools
from qutip import basis, tensor, snot
def prepareMeasurement(N, psi):
# all the spin configurations
confs = list(itertools.product([0, 1], repeat=N))
# probability distribution
P = []
for conf in confs:
# particular outcome as quantum object
psi_ref = tensor([basis(2, m) for m in conf])
# probability of this outcome
p = np.abs(psi.overlap(psi_ref))**2.
# append to the distribution
P.append(p)
return confs, np.array(P)
Then a function that given this amplitude takes n random measurements.
def simulateMeasurement(confs, P, n):
return np.random.choice(range(len(confs)), n, p=P)
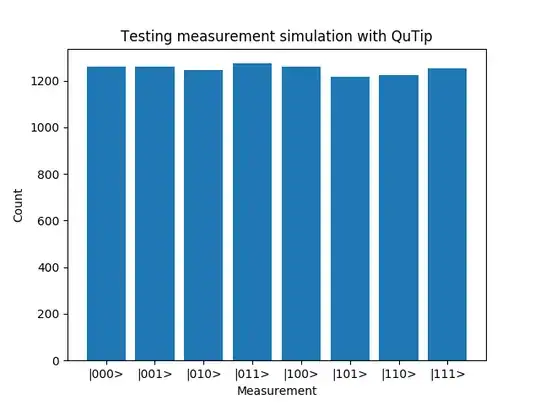
We can test it on a little example, let's create an even superposition of all the eigenstates. They should all have same amplitudes.
psi0 = tensor([basis(2, 0), basis(2, 0), basis(2, 0)])
psif = snot(N=3, target=0)*psi0
psif = snot(N=3, target=1)*psif
psif = snot(N=3, target=2)*psif
And this is how we apply our measurement simulation, let's perform 10000 measurements. Let's also calculate counts.
confs, P = prepareMeasurement(3, psif)
measurements = simulateMeasurement(confs, P, 10000)
unique, counts = np.unique(measurements, return_counts=True)
Visualize the data in histogram-like form.
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.bar(unique, height=counts)
plt.xticks(unique, ["|{0}>".format(format(m, '03b')) for m in unique])
ax.set_title('Testing measurement simulation with QuTip')
ax.set_ylabel('Count')
ax.set_xlabel('Measurement')
plt.show()
This is what we're getting
I included everything in this public gist repository. Hope it helps!
Main purpose of Qutip is to explore dynamics of quantum systems and therefore density matrices are the tool to use. According to this answer on Quantum computing, we can model a measurement operator Pi on a density matrix. In the case of the measurement of a single qubit in the computational basis, you have $$P_0=|0\rangle\langle 0|\qquad P_1=|1\rangle\langle 1|$$
If you want to talk about n qubits where you measure just the first one, then you use the measurement operators
$$P_0=|0\rangle\langle 0|\otimes\mathbb{I}^{\otimes(n-1)}\qquad P_1=|1\rangle\langle 1|\otimes\mathbb{I}^{\otimes(n-1)}$$
Implementation with the Qutip dag method. First we set up a two level quantum system with the basis method use a vector v0 for the zero vector and v1 for one vector.
v0 = qp.basis(2, 0)
Calculate outer product with the dag method this will give a density operator
P0 = v0 * v0.dag()
expand for multiqubit gate
M0 = qp.gate_expand_1toN(P0, self.activeQubits, qubitNum)
Also
v1 = qp.basis(2, 1)
You can find a basic qubit quantum simulator running on Qutip in the SimulaQron software.
