Expected repetitions of the quantum part of Shor's algorithm

Question

Shor's algorithm to factor a number $N$ goes as follows:

1. Pick a random value $b \in (0, N)$.
2. Use a specific quantum computation to a sample a value $v$ that should be close to $2^{m} k/p$ where $m$ is a precision parameter of the quantum computation, $p$ is the period of $f(x) = b^x \pmod{N}$, and $k$ is an unknown integer resulting from the sampling process.
3. Convert $v$ into a potential period $p$ using an algorithm based on continued fractions.
4. If $b^p \neq 1 \pmod{N}$, goto 1. The period finding process failed (e.g. maybe you got $v=0$).
5. If $p$ is odd, goto 1. You got a useless period. Try a different $b$.
6. If $b^{p/2} \equiv -1 \pmod{N}$, goto 1. You got a useless period. Try a different $b$.
7. Output $\gcd(b^{p/2} - 1, N)$

My question is: how often do steps 4, 5, or 6 fail? Assuming an ideal quantum computer with no error, how often do you just get unlucky and pick a bad $b$ or sample a bad $v$? How many times do you expect to repeat step 2 before the factoring succeeds?

References giving numerical upper bounds on the 4-5-6 failure chance would be especially appreciated.

Answer 1

The number of runs required is arbitrarily close to 1, using the correct post-processing. See "On the success probability of quantum order finding" by Martin Ekerå from Jan 2022:

We prove a lower bound on the probability of Shor's order-finding algorithm successfully recovering the order r in a single run. The bound implies that by performing two limited searches in the classical post-processing part of the algorithm, a high success probability can be guaranteed, for any r, without re-running the quantum part or increasing the exponent length compared to Shor. Asymptotically, in the limit as r tends to infinity, the probability of successfully recovering r in a single run tends to one. Already for moderate r, a high success probability exceeding e.g. $1-10^4$ can be guaranteed. As corollaries, we prove analogous results for the probability of completely factoring any integer N in a single run of the order-finding algorithm.

Answer 2

This self-answer gives a not-very-good worst case analysis. I'd really rather have a proper distribution of repetition counts.

Probability of a period resulting in factoring

In Shor's original paper, you can find the following statement:

The multiplicative group (mod $p^α$) for any odd prime power $p^α$ is cyclic [Knuth 1981], so for any odd prime power $p_i^{a_i}$, the probability is at most 1/2 of choosing an $x_i$ having any particular power of two as the largest divisor of its order $r_i$. Thus each of these powers of 2 has at most a 50% probability of agreeing with the previous ones, so all k of them agree with probability at most $1/2^{k−1}$, and there is at least a $1 - 1/2^{k-1}$ chance that the $x$ we choose is good. This scheme will thus work as long as $n$ is odd and not a prime power; finding factors of prime powers can be done efficiently with classical methods

(Oddly, I also found an older version of the paper with a bound of $1-2^{-k}$ instead of $1-2^{1-k}$. Might be an error that was corrected?)

This implies a 50% chance of success of getting a good period (steps 4+5), since all numbers have at least two distinct factors or else can be factored classically.

Probability of a sample determining a period

For getting a good sample (step 3), Shor gives a more complicated bound. If you sample a value with a $k$ that's not relatively prime to the period, the period you recover will be wrong. But integers have a limited number of divisors, and Shor cites a bound:

There are also $r$ possible values for $x^k$, since $r$ is the order of $x$. Thus, there are $r \phi(r)$ states which would enable us to obtain $r$. Since each of these states occurs with probability at least $\frac{1}{3r^2}$, we obtain $r$ with probability at least $\frac{\phi(r)}{3r}$. Using the theorem that $\phi(r)/r > k/\log \log r$ for some fixed $k$ [17, Theorem 328], this shows that we find $r$ at least a $k/ \log \log r$ fraction of the time.

[17]: G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers, Fifth Edition, Oxford University Press, New York (1979).

We know $r < N$, so this proves step 3 introduces at most $O(\lg \lg N)$ repetitions. It seems likely to me that this can be improved (e.g. if you keep replacing $b$ by $b^p$ when you get a bad $p$ that would presumably keep reducing $r$, or maybe that's bad?), and I'm sure someone has explained how to do this in great detail, but I don't know the reference.

"On Shor's Quantum Factor Finding Algorithm: Increasing the Probability of Success and Tradeoffs Involving the Fourier Transform Modulus" seems promising. It discusses using the lcm of two samples in order to get a constant probability of successfully recovering a period (~60%).

---

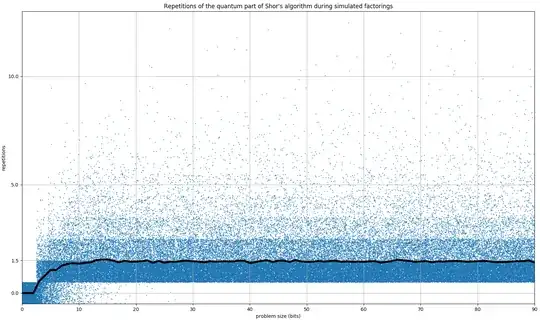
I also did some simulation of how many repetitions are needed when the two factors are similarly sized primes, using some basic post-processing, and it appears to converge to 1.5. The following plot is showing a blue dot for each factoring attempt, with a random +-0.5 on each dot's X and Y position so you get a sense of the density in each area. The thick black line is the average.