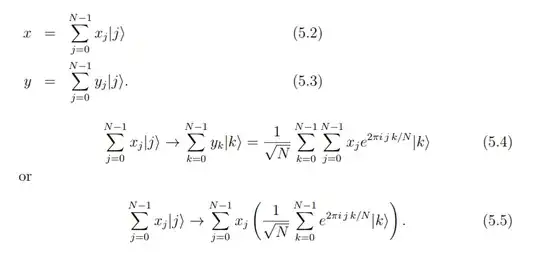How to describe, or encode, the input vector x of Quantum Fourier Transform?

Question

Firstly, I'd like to specify my goal: to know why QFT runs exponentially faster than classical FFT. I have read many tutorials about QFT (Quantum Fourier Transform), and this tutorial somehow explains something important between classical and quantum Fourier Transform.

Inside 1, it describes that:

The quantum Fourier transform is based on essentially the same idea with the only difference that the vectors x and y are state vectors (see formula 5.2, 5.3),

However, I couldn't catch up the statement regarding "x and y are state vectors"; I get stuck at the formula 5.2 and 5.3. I want to know how to convert the classical input vector x to the right hand side of the formula 5.2. If this confusing problem is solved, it'll be better for me to understand the time complexity issue of QFT.

Answer 1

Formula 5.2 refers to an encoding we call amplitude encoding. Imagine you have a vector $x$ with components $x_i$, the components are then encoded as amplitudes of a quantum state.

This encoding is very important as a vector that has a dimension $N$, will be encoded in quantum form using about $log(N)$ qubits. This is the main reason why in many quantum algorithms using this encoding we can achieve exponential speedup in the size of the problem.

However, generally in quantum computing, you have to assume that this encoding is done using a device called quantum random access memory for loading in this form a vector. Or you are given a circuit that do the job for you.

Answer 2

You don't convert a classical input to the r.h.s. of Eq. (5.2). The r.h.s. of Eq. (5.2) is something you get as the output of a preceding quantum computation as a quantum state, such as in Shor's algorithm. This is the only way to get an exponential speedup -- if you had to start from an exponentially big classical vector, there would be no way to solve this in polynomial time.