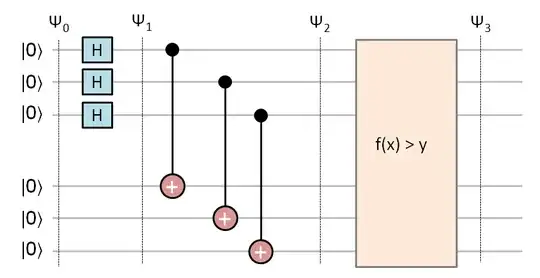
Let $U$ be the circuit you stated that takes $| 0 \rangle^{\otimes (2n)}$ to $\psi=\frac{1}{2^{n/2}}\sum_{i=0}^{2^n-1} | i \rangle \otimes | f(i) \rangle $.
$S_\psi = I - 2 | \psi \rangle \langle \psi | = U ( S_{| 0 \rangle^{\otimes (2n)}} ) U^\dagger$
$S_P$ needs to be the unitary that sends $| i \rangle \otimes | j \rangle$ to $(-1)^{j>y} (| i \rangle \otimes | j \rangle)$. For example if $y$ is $2^{n-1}-1$, then this would be done with a $Z$ gate on the most significant index. Generally for $y$ 1 less than a power of $2$ this should be easy by combining information from all more significant indices.
Those are the requisite ingredients for amplitude amplification for $f(x) \geq 2^k$ for some $k$. The number of times you need to apply $Q$ is dependent on the overlap which is dependent on how many solutions $x$ there are to $f(k) \geq 2^k$. If $f$ is reversible so just giving a permutation of $2^n$, then you have the overlap in terms of $n-k$ without bothering with any details of $f$.
You won't get exactly the result you asked for because that was projecting to a subspace/not unitary, but this will get you close to that desired state given your starting setup. There is also the trouble of setting $y$ arbitrarily, but at least you can amplify the condition $f(x) \geq 2^k$ as a step along the way to amplifying $f(x) \geq y$ for $y \geq 2^k$.
I may have misunderstood the question. You might have wanted something that works more generally, but given your small example this approach is okay. You don't have to worry about the fact that $\frac{\pi}{4\theta}$ will get really big as $n$ grows you, if you don't let $n$ grow. Did you want to input $y$ as a quantum state as well?
I wasn't careful about checking $\geq$ vs $\gt$ so you should check that.