I'm working through Scott Aaronson's Quantum Information Science problem sets, and I'm having trouble with a specific problem in ps5 (PDF). Specifically the following problem:
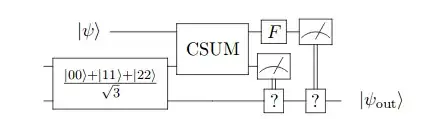
A “qutrit” has the form $a|0\rangle+b|1\rangle+c|2\rangle$, where $|a|^2+|b|^2+|c|^2=1$. Suppose Alice and Bob share the entangled state $(|00\rangle+|11\rangle+|22\rangle)/\sqrt 3$. Then consider the following protocol for teleporting a qutrit $|\psi〉=a|0\rangle+b|1\rangle+c|2\rangle$ from Alice to Bob: first Alice applies a CSUM gate from $|\psi〉$ onto her half of the entangled pair, where
$$\operatorname{CSUM}(|x\rangle\otimes|y\rangle) =|x\rangle\otimes|y+x \bmod 3\rangle$$
Next, Alice applies the unitary matrix $F$ to the $|\psi\rangle$ register, where
$$F=\frac{1}{\sqrt{3}}\begin{bmatrix}1&1&1\\1&\omega&\omega^2\\1&\omega^2&\omega^3\end{bmatrix}$$
and $\omega=e^{2i\pi/3}$ so that $\omega^3= 1$. She then measures both of her qutrits in the $\{|0\rangle,|1\rangle,|2\rangle\}$ basis, and sends the results to Bob over a classical channel. Show that Bob can recover a local copy of $|\psi\rangle$ given these measurement results.
This quantum circuit summarizes the protocol:
Here the double-lines represent classical ‘trits’ being sent from Alice to Bob. Depending on the value of 0, 1 or 2 Bob can apply a ? gate 0, 1, or 2 times. Prove that $|\psi〉=|\psi_\text{out}\rangle$ for appropriately chosen ? gates for all possible measurement results. Hint: You could explicitly work out all 9 possible cases, but you could also save time by noticing a general pattern that lets you handle all the cases in a unified way.
Here's what I've done: after applying the CSUM gate to the mixed state of three qutrits, Alice and Bob share the state: \begin{align*} & \frac{a}{\sqrt{3}}(|000 \rangle + |011 \rangle + |022 \rangle) \\ + & \frac{b}{\sqrt{3}}(|110 \rangle + |121 \rangle + |102 \rangle) \\ + & \frac{c}{\sqrt{3}}(|220 \rangle + |201 \rangle + |212 \rangle) \end{align*} After Alice applies $F$ to the first qutrit in the shared state, they're left with: \begin{align*} & \frac{|00 \rangle}{3}(a|0 \rangle + c|1 \rangle + b|2 \rangle)\\ + & \frac{|01 \rangle}{3}(b|0 \rangle + a|1 \rangle + c|2 \rangle)\\ + & \frac{|02 \rangle}{3}(c|0 \rangle + b|1 \rangle + a|2 \rangle) \\ + & \frac{|10 \rangle}{3}(a|0 \rangle + w^2c|1 \rangle + wb|2 \rangle)\\ + & \frac{|11 \rangle}{3}(wb|0 \rangle + a|1 \rangle + w^2c|2 \rangle)\\ + & \frac{|12 \rangle}{3}(w^2c|0 \rangle + wb|1 \rangle + a|2 \rangle)\\ + & \frac{|20 \rangle}{3}(a|0 \rangle + wc|1 \rangle + w^2b|2 \rangle) \\ + & \frac{|21 \rangle}{3}(w^2b|0 \rangle + a|1 \rangle + wc|2 \rangle) \\ + & \frac{|22 \rangle}{3}(wc|0 \rangle + w^2b|1 \rangle + a|2 \rangle) \\ \end{align*}
So after Alice measures her qutrits, whatever is inside the parenthesis is the state that Bob holds. However, I don't wee what operations can be used multiple times to "fix" the output.
It seems to me that Alice could communicate to Bob with one trit which two coefficients need to be transposed, and use one trit to tell Bob how to fix the remaining $w$'s. That doesn't seem to fit the desired protocol though, making me doubt the computations that I have performed above. If anyone could help me out (or point out a better approach), it would be appreciated. Thanks!