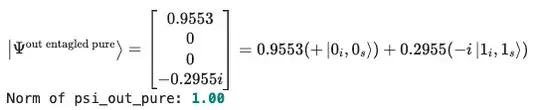I am trying to simulate Type I and Type II Spontaneous Parametric Down-Conversion (SPDC) based on "Chapter 9 Optical test of quantum mechanics" of the book Introductory Quantum Optics. The result for Type I is true, but for Type II, I got four terms instead of three terms.
Here are my codes for both types:
Type I:
def hamiltonian_none_degenerate_spdc_classical_pump_type_I(Fk_dim, g_spdc):
a_i_spdc = qt.destroy(Fk_dim) & qt.qeye(Fk_dim)
a_s_spdc = qt.qeye(Fk_dim) & qt.destroy(Fk_dim)
H_spdc = g_spdc * (a_i_spdc.dag() @ a_s_spdc.dag())
H_spdc += H_spdc.dag()
U_spdc = (-1j * H_spdc).expm()
return U_spdc, a_i_spdc, a_s_spdc
This is my result for Fock dimension = 2 and mu = 0.3 same as (9.9):
Type II:
def hamiltonian_none_degenerate_spdc_classical_pump_type_II(Fk_dim, g_spdc):
a_H_i_spdc = qt.destroy(Fk_dim) & qt.qeye(Fk_dim) & qt.qeye(Fk_dim) & qt.qeye(Fk_dim)
a_V_i_spdc = qt.qeye(Fk_dim) & qt.destroy(Fk_dim) & qt.qeye(Fk_dim) & qt.qeye(Fk_dim)
a_H_s_spdc = qt.qeye(Fk_dim) & qt.qeye(Fk_dim) & qt.destroy(Fk_dim) & qt.qeye(Fk_dim)
a_V_s_spdc = qt.qeye(Fk_dim) & qt.qeye(Fk_dim) & qt.qeye(Fk_dim) & qt.destroy(Fk_dim)
H_spdc = g_spdc * (a_H_i_spdc.dag() @ a_V_s_spdc.dag() + a_H_s_spdc.dag() @ a_V_i_spdc.dag())
H_spdc += H_spdc.dag()
U_spdc = (-1j * H_spdc).expm()
return U_spdc, H_spdc, a_H_i_spdc, a_V_i_spdc, a_H_s_spdc, a_V_s_spdc
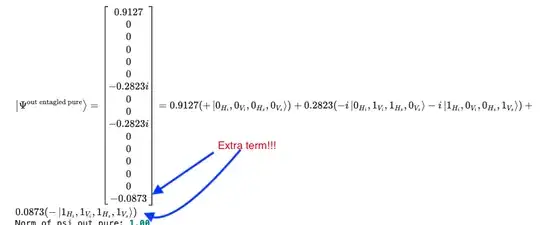
This is my result for Fock dimension = 2 and mu = 0.3 it should be same as (9.11):
Where is the issue for the Hamiltonian of Type II?