Why Must We Remove Garbage for Interference Tests? Graph Isomorphism example

Question

I am curious about quantum approaches to graph isomorphism and have encountered a recurring point: the necessity of cleaning up any garbage generated during state preparation. For example, take a look at this answer or this answer. They suggest that without un-computing the garbage, interference-based tests (such as the SWAP or Hadamard tests) will not work correctly. However, I'm still unclear on the detailed reasoning behind this requirement.

To illustrate, consider the following scenario, in which I am given the adjacency matrix of a graph, $G$, binary-encoded in a register, $g$, and two operators:

1. Operator $\mathbf{A}$ – Permutation Superposition I have an operator $\mathbf{A}$ that creates a uniform superposition over all binary encodings of the $n!$ permutations of a bitstring of length $n$ on register $a$. This operator prepares a state that ideally represents all possible permutation encodings in superposition.

2. Operator $\mathbf{B}$ – Data Operations. Next, I use an operator $\mathbf{B}$ which, based on the bitstrings produced by $\mathbf{A}$, applies a fixed sequence of operations to a data register. (For example, if qubit 0 is in state $|1\rangle$, then swap columns $i$ and $j$ of $g$.) Importantly, these operations are defined solely by the permutation encoding and are independent of the graph's adjacency matrix or any other data details.

After applying these two operators, I obtain a uniform superposition over all the possible permutation of $G$ encoded in $g$.

My question is: Why can’t I apply interference tests (like the SWAP or Hadamard tests) using this circuit? Is the register $a$ considered ancillary? And if so, why? Can someone provide an intuitive explanation or a simple mathematical example that illustrates how the leftover garbage distorts the measurement outcomes?

Answer 1

Your understanding is perfectly correct up until the last step.

Let $G$ be an unweighted graph on $n$ vertices. Let $g$ be an $n^2$ adjacency matrix of $G$.

1. It is easy to prepare a state $|g\rangle$ on $n^2$ qubits in a first register. This can be in the computational basis for now; that is fine. You don't name this operator but it's pretty straightforward. Just set the indexed qubits to be $|0\rangle$ or $|1\rangle$ as needed based on the adjacency matrix $g$.
2. You are right that it also "easy" to prepare another state $\frac{1}{\sqrt{n!}}\sum|\pi_i\rangle$ of all $n!$ different permutations in a second regiter. You call this register $\bf{a}$, and the operator $\bf{A}$.
3. You are also right that it "easy" to apply each of the $n!$ permutations in the second register to the first register. You call this operator $\bf B$.
4. After applying the above, you are left with the state $\frac{1}{\sqrt{n!}}\sum|\pi_i(g)\rangle|\pi_i\rangle$ in the first and second registers. This looks very attractive, and almost what you want! To use your language, it is indeed the "uniform superposition over all the possible permutations of $G$ encoded in $g$.
5. Indeed, we can do the same for another graph $H$ to prepare $\frac{1}{\sqrt{n!}}\sum|\pi_i(h)\rangle|\pi_i\rangle$. It is so tempting to just do a SWAP test between the two!
6. But, how do you uncompute the second register $|\pi_i\rangle$ after you've prepared the uniform superposition and then subsequently applied the permutations to $g$? with your operator $\bf B$?

This last step needs to be done in order to have any chance of creating the requisite interference - it is the $|\pi_i\rangle$ register that is the "garbage"; using your language it is indeed the register $a$ that is ancillary, and would block the interference in any Hadamard or SWAP test.

Recall that in $\frac{1}{\sqrt{n!}}\sum|\pi_i(g)\rangle|\pi_i\rangle$ the first and second registers are entangled. So to uncompute the second register you must also act on the first register, but as far as I'm aware no one knows how to do that without also destroying the superposition in the first register, which you worked so hard to do in the first place.

---

It might be fun or pedagogically worth-while to spell out on pencil-and-paper, in some excruciating detail, what goes wrong even for $n=3$ with, say, a graph consisting of a first isolated vertex and a second and third vertex connected by a common edge. $S_3$ only has six elements, and there are only $3^2=9$ different qubits to store the adjacency matrix.

Answer 2

^{(CW to expand on other answer.)}

---

We will try to apply this approach to two labeled graphs $G$ and $H$ on three vertices as below. We wish to quantumly test whether these graphs are isomorphic, by preparing two states $|G\rangle$ and $|H\rangle$ corresponding to the uniform superposition of all permutations of $G$, respectively $H$. We'll see what happens when we do a SWAP test therebetween.

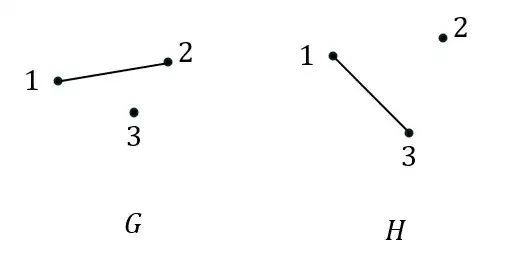
Let's go in order; we'll begin with graph $G$, and then later work on graph $H$. At the end we will see what happens when we SWAP them.

1. Let's prepare a first register $|g\rangle$, where $g$ is the adjacency matrix of $G$. Let's let $\mathbf{G}$ be the operator that prepares $|g\rangle$ from the all-zero's ket, e.g., $\mathbf{G}|00\cdots0\rangle=|g\rangle$.

$$g=\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}.$$

2. In another register, let's also apply the operator $\mathbf{A}$ to prepare the uniform superposition over all $n!$ elements of $S_n$ in another register, starting with a register initialized to the all-zero's ket $|00\cdots0\rangle$; we will use cycle notation. It's (mostly) mechanical to do this with something like Grover-Rudolph and/or Stirling's Approximation. But with only $n=3$ vertices, there are only six elements to $S_3$:

$$\mathbf{A}|00\cdots0\rangle=\frac{1}{\sqrt 6}\big(|(1)\rangle+|(12)\rangle+|(13)\rangle+|(23)\rangle+|(123)\rangle+|(132)\rangle\big).$$

3. Now, let's apply, in superposition, operator $\mathbf B$ on the first and second registers. This does the appropriate permutation to $g$ over all such permutations stored in the second register. You suggest applying a conditional SWAP between columns $i$ and $j$ - I would do something like that too, but I think you'd also need to SWAP the rows as well. But it doesn't matter too much how this operator $\mathbf B$ is implemented; it's reversible and scales gracefully with $n$, and its implementation is also mechanical.

4. In particular, after applying $\mathbf B$ and $\mathbf{A}$ to the registers, we will have $\mathbf{B}\mathbf{A}\mathbf{G}|00\cdots0\rangle|00\cdots0\rangle=|G\rangle$, where, assuming I did my permutations correctly:

$$|G\rangle=\frac{1}{\sqrt 6}\big( |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|(1)\rangle+ |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|(12)\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|(13)\rangle+ |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|(23)\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|(123)\rangle+ |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|(132)\rangle\big). $$

5. Let's now do exactly steps 1-4 above, but for $h$ instead of $g$. That is, we will prepare $|H\rangle$ by acting on $\mathbf{B}\mathbf{A}\mathbf{H}|00\cdots0\rangle|00\cdots0\rangle$, which, if I permuted correctly, gives: $$|H\rangle=\frac{1}{\sqrt 6}\big( |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|(1)\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|(12)\rangle+ |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|(13)\rangle+ |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|(23)\rangle+ |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|(123)\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|(132)\rangle\big). $$

6. Lining up the matrices or alternatively lining up the permutations and taking the dot product lets us visually see that $\langle H|G\rangle=0$. Thus, the SWAP test between $|G\rangle$ and $|H\rangle$ won't tell you anything!

7. In the comments it was also suggested to apply $\mathbf{H}^\dagger\mathbf{A}^\dagger\mathbf{B}^\dagger\mathbf{B}\mathbf{A}\mathbf{G}|0\rangle|00\cdots0\rangle$. But this is equal to $\mathbf{H}^\dagger\mathbf{G}|00\cdots0\rangle$, which is also going to be junk.

8. Really what you need is another operator, call it, say, $\mathbf{T}$ for tigerjack, that uncomputes the second register back down to the all-zeroes ket. That is, ideally we'd like $\mathbf{T}\mathbf{B}\mathbf{A}\mathbf{G}|00\cdots0\rangle|00\cdots0\rangle$ to give:

$$|G'\rangle=\frac{1}{\sqrt 6}\big( |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle\big). $$

10. If we had such an operator, we could apply $\mathbf{T}\mathbf{B}\mathbf{A}\mathbf{H}|00\cdots0\rangle|00\cdots0\rangle$ to get:

$$|H'\rangle=\frac{1}{\sqrt 6}\big( |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle+ |\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}\rangle|00\cdots0\rangle\big). $$

11. If I did it right (there's a good chance I made a mistake) we see that $\langle H'|G'\rangle=1$! But no one knows how to make any such $\mathbf{T}$ for general $n$ that runs in polynomial time.

^{It's been a challenge for about 30 years to find such an operator $\mathbf{T}$ that resets the permutation register to $|00\cdots0\rangle$. Then again, some people think Babai's quasi-polynomial classical algorithm makes this algorithmic exploration less attractive. Personally, for me I like to spend more time thinking about ways to instantiate the 31-year-old Simon's oracle or the 28-year-old Welded Trees oracle, etc.}