TL/DR: With $t$ being the classical mixing time of an connected, non-bipartite, unweighted, undirected graph on $n$ vertices, and $\pi_n=\frac{1}{n}$ being the stationary probability at vertex $v_n$, what strategy, if any, is there to interpolating between (a) classical SWAP gates and (b) quantum square-root-of-SWAP gates such that (1) the probability $\pi_n'$ of a quantum walk that starts at $|v_1\rangle=|100\cdots00\rangle$ and lands on vertex $|v_n\rangle=|000\cdots01\rangle$ with probability $\pi_n'$ that is also about $\frac{1}{n}$, (2) in a time $t'$ that is polynomially less than the classical mixing time, preferably $O(\sqrt t)$?
Can we get the effect of both classical mixing behavior of settling to a stationary distribution and also the effect of a more rapid exploration of a graph with a continuous-time quantum walk? What's the relationship, if any, between the stationary distribution of such a hybrid classical/quantum walk, and the hitting time of said walk?
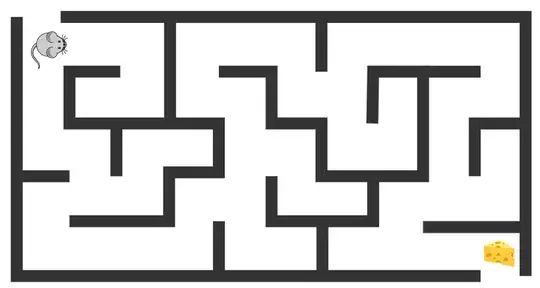
Now I describe the problem with flavor text about Finks the Rat. (Don't worry; no animals are going to be harmed in this experiment.)
Suppose we place Finks in $v_1$, the top-left corner of an $n=60$-room maze; let's also put some cheese at $v_n$, the bottom right.
We want to see how long it takes for Finks to find the cheese, but poor Finks has been having a head-cold lately and she can't smell so easily; all she can do is randomly walk from room to room.
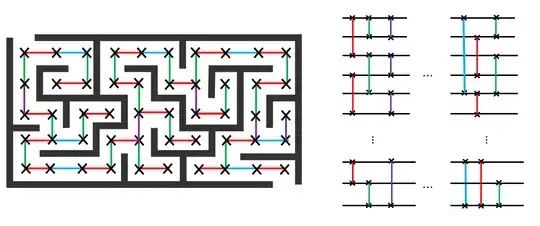
Let's help her out by edge-coloring each passageway with one of $4$ colors, red, green, light blue, or purple. Finks can randomly choose which color passageway she wishes to take (she can flip a classical, four-sided die to make the choice of each door).
We can model her behavior by placing SWAP gates along the passageway from room to room and having her randomly decide whether to do a red layer, a green layer, a purple layer, or a light blue layer at each step.
By the celebrated Perron-Frobenius theorem Finks should eventually be able to find the cheese after time $t$. After the mixing time $t$ the probability $\pi_n$ of her being in the room with the cheese, $v_n$, is inverse-proportional to the number of rooms in the maze - e.g., $1/60$; it just might take her some time $t$ to get there.
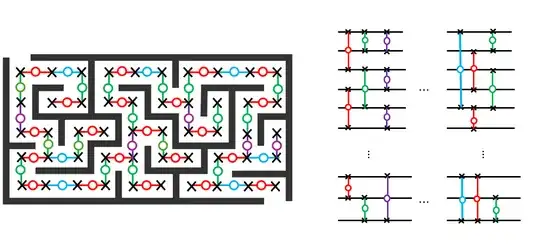
But even though she's been fighting a cold lately, Finks also has quantum superpowers. So she can still flip her classical four-sided die to decide which color hallway to walk, but instead of doing classical SWAP gates, she can perform some quantum square-root-of-SWAP gates.
Depending on the maze, a quantum Finks will be able to have a good probability of finding the cheese at least polynomially faster, in time $O(\sqrt t)$.
However, it's also well-known that because of unitarity, such continuous-time quantum walks don't have the same well-defined stationary distribution. Indeed after the same time $t$ as in the classical case, the room with the cheese in it may have seen a lot of destructive interference and may be at an antinode; poor Finks might miss her chance at time $t$.
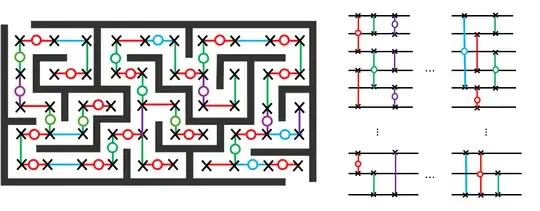
Finks is pretty smart, though, and she comes up with an idea. She decides to try to get the best of both classical and quantum behavior. So sometimes she will do a classical SWAP and sometimes she'll do a quantum SWAP as below:
By sometimes doing a classical SWAP and sometimes doing a quantum SWAP, can Finks get the best of both the classical world and the quantum world, finding the cheese faster but also being more likely to have settled into a stationary distribution? If so, what is the best way for her to get a stationary probability $\pi_n'$ preferably in $O(1/n)$, but also in the fastest time $t'$, preferably $O(\sqrt t)$?