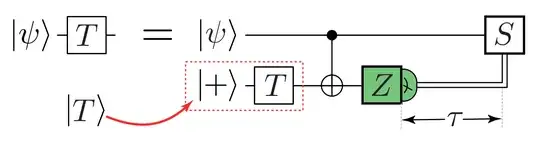
In the T gate teleportation circuit shown below, it is said that we have to finish decoding to determine the correct logical measurement outcome of a Z measurement. I am confused whether we have to finish decoding of the transversal CNOT gates right before the Z measurements. Do we have to repeat syndrome measurement $d$ times (for surface code, for example) after the transversal CNOT gates in both the two blocks and decode them, or do we only have to decode the Z measurement outcomes obtained by transversal physical Z measurements to determine whether to apply the S gate? In other words, how many rounds do we have wait from when the transversal CNOT gates finish until we can start the decoding?
1 Answers
All you care about here is to be able to measure the right value of your $Z$ operator before applying the classically controlled $S$ gate.
This means that you at least need to catch errors that may change the value of the logical state of the bottom qubit. Detecting an error can be done by ensuring that you have enough detectors to isolate the error in time. Intuitively, I would say that $d$ rounds are indeed necessary after the CNOT, since you want to preserve the code properties of error detection.
In a general case, you would need to decode both qubits. However, assuming that your decoder favours independent errors (e.g. MWPM), then you can in practice decode both independently. You would only feed syndromes related to the bottom qubit into your decoder (after logical measurement). That way, you may also detect an error that would have propagated through the CNOT when you decode the top part.
I believe that the time $\tau$ hints at the fact that decoding is performed on the measured qubit and you have to keep measuring syndromes for the top qubit.
Also note that the way you detect and correct for errors can influence whether you perform extra rounds of syndrome measurements or not:
- If you constantly decode and correct errors by applying actual quantum gates, you may trust your logical measurement, up to measurement errors. Note that applying gates may increase the physical error rate, so this is usually not an optimal solution.
- If you only decode and correct when performing logical measurements, then you will need to use the measurements in the $Z$ measurement to construct your detector model and decode. The correction can be applied at the "software" level when you decide to apply or not your $S$ gate.
- 440
- 2
- 10