Measuring X-stabilizers in Surface codes

Question

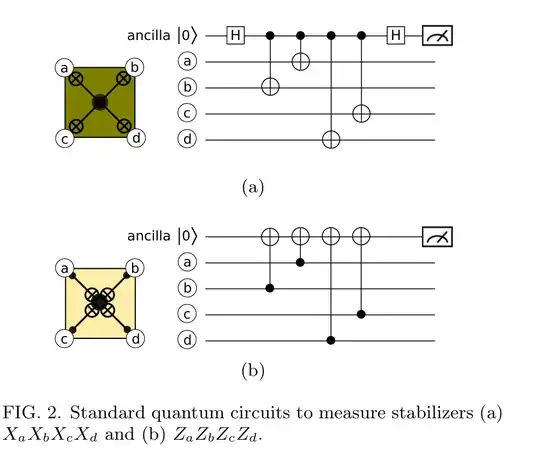
I am trying to measure stabilizers in a surface code, a common circuit to measure stabilizers look like this: https://arxiv.org/pdf/1404.3747

The problem is when Measuring the X-stabilizer circuits in Qiskit (python). It returns nothing useful. Take the following code snippet which implement fig 2a's circuit:

ar_z = QuantumRegister(1, 'ar_z')
cr_z = ClassicalRegister(1, 'cr_z')
dr = QuantumRegister(4, 'd')
qc = QuantumCircuit(ar_z,dr, cr_z)
qc.h(ar_z[0])
qc.cx(ar_z[0], dr[1])
qc.cx(ar_z[0], dr[0])
qc.cx(ar_z[0], dr[3])
qc.cx(ar_z[0], dr[2])
qc.h(ar_z[0])
qc.measure(ar_z, cr_z)
simulator = AerSimulator()
result = simulator.run(qc).result()
print(result.get_counts())
qc.draw(output='mpl')
plt.show()

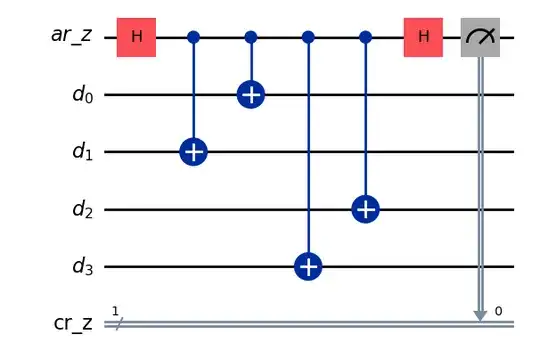
Drawing the output:

And the resutls: {'1': 536, '0': 488}

This tells me nothing useful about the ancilla or weather an error was induced on one of the data qubits. My thoughts was that if a z-error was induced on one of the qubits, the ancilla would return 1? else 0. Is this not the case? if so How do I measure the X-stabilizers?

Answer 1

You're not measuring a stabilizer here (not in the sense that your measurement is supposed to be deterministic), because your register $d$ starts in the $|0\rangle^{\otimes 4}$ quantum state and not a valid logical quantum state.

Before the measurement can be observed as deterministic, you have to project $d$ into the codespace. This can be done with an encoding circuit, or by first measuring all the code stabilizers once.

You observe a 50%/50% repartition, just as if you measured the state $|0\rangle$ in the $X$ basis for the first time. Note that $Z$-stabilizers already stabilize the $|0\rangle^{\otimes n}$ state, so it is only necessary to measure the $X$-stabilizers once to project the register into the codespace.

Consider the following circuit:

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit_aer import AerSimulator
import matplotlib.pyplot as plt
ar_z = QuantumRegister(2, 'ar_z')
cr_z = ClassicalRegister(2, 'cr_z')
dr = QuantumRegister(4, 'd')
qc = QuantumCircuit(ar_z,dr, cr_z)
qc.h(ar_z[0])
qc.cx(ar_z[0], dr[1])
qc.cx(ar_z[0], dr[0])
qc.cx(ar_z[0], dr[3])
qc.cx(ar_z[0], dr[2])
qc.h(ar_z[0])
qc.z(dr[1])  # Uncomment to add Pauli error and see changes
qc.h(ar_z[1])
qc.cx(ar_z[1], dr[1])
qc.cx(ar_z[1], dr[0])
qc.cx(ar_z[1], dr[3])
qc.cx(ar_z[1], dr[2])
qc.h(ar_z[1])
qc.measure(ar_z, cr_z)
simulator = AerSimulator()
result = simulator.run(qc).result()
print(result.get_counts())
qc.draw(output='mpl')
plt.show()

It repeats your measurement protocol, and you can check that the $X$-stabilizer measurements are now deterministic starting from the second. Adding a $Z$ Pauli error in-between the two measurements indeed flips the second measurement, so it successfully detects a Pauli $Z$ error.

In a true simulation, you do not want to add the $Z$ errors manually, but to rely on the simulator to randomly add noise according to a defined noise model.