Why logical error rates from BP-OSD and MWPM are so different?

Question

I'm plotting logical error rates for different codes and comparing two decoders (BP-OSD and MWPM) 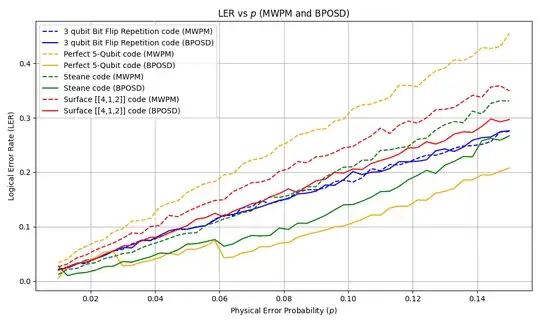For each code I calculate logical error rates by preparing the code in $|0\rangle_L$ state with encoding circuit ($p_{L_0}$), measuring stabilizers and measuring logical $Z$ and preparing the code in $|+\rangle_L$ state, measuring stabilizers and measuring logical $X$ ($p_{L_+}$). Then what's plotted here is $p_{L} = p_{L_0} + p_{L_+}$. Here are the example circuits I would use for estimating $p_L$ of 5-qubit code: 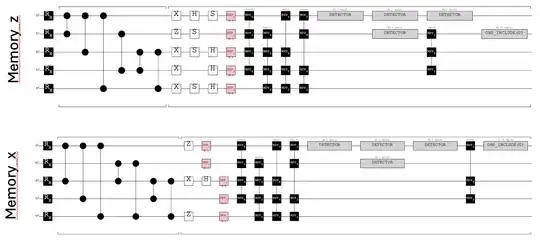Let me know if these circuits look right to you. I know normally one does several rounds on syndrome measurements but I'm only interested in comparing capabilities of the codes so I'm hoping one round of syndrome measurements should suffice. For clarity here are the same circuits but presented differently

circ_mem_z = stim.Circuit('''RX 0 1 2 3 4
TICK
CZ 0 1 0 2 0 4 1 3 2 3 2 4
TICK
X 0 2 3 4
Z 1
S 1 2 4
H 0 2 3 4
S 0
DEPOLARIZE1(0.1) 0 1 2 3 4
MPP X0*Z1*Z2*X3 X1*Z2*Z3*X4 X0*X2*Z3*Z4 Z0*X1*X3*Z4
DETECTOR rec[-1]
DETECTOR rec[-2]
DETECTOR rec[-3]
DETECTOR rec[-4]
MPP Z1*X2*Z3
OBSERVABLE_INCLUDE(0) rec[-1]''')
circ_mem_x = stim.Circuit('''
RX 0 1 2 3 4
TICK
CZ 0 2 0 3 0 4 1 2 1 4 2 3 2 4
TICK
X 2
Z 0 4
H 2
DEPOLARIZE1(0.1) 0 1 2 3 4
MPP X0Z1Z2X3 X1Z2Z3X4 X0X2Z3Z4 Z0X1X3Z4
DETECTOR rec[-1]
DETECTOR rec[-2]
DETECTOR rec[-3]
DETECTOR rec[-4]
MPP Z0X2X3
OBSERVABLE_INCLUDE(0) rec[-1]''')

Answer 1

What you are noticing is that MWPM performs worse for the Steane and perfect codes than BP-OSD, while their performance is closer for the repetition code and the surface code. This is expected behavior.The Steane and perfect codes are not "matchable", hence MWPM performs badly. A code is "matchable" when error mechanisms trigger two detectors. As an example, an error on the first qubit for the Steane code only triggers one stabilizer.

Stim decomposes edges into graphlike errors if you use decompose_errors=True when compiling your DEM, but for general codes this will not be great.

OSD on the other hand inverts a submatrix of the parity check. If you use BP+OSD it will invert the submatrix with the highest pseudopriors output from BP. So it sort of works for general codes, especially if you increase the size of the submatrix it inverts by increasing the OSD order. What order of OSD are you using? The problem with OSD in general is its complexity, as the complexity of OSD- $w$ is: $O(n^3+ 2^w n)$.

In general, low OSD iterations won't work very well for codes with many short cycles in their Tanner graph. If you instead consider circuit level noise, the cycles often become larger, so it might perform better.

Edit: I used default order=2 for BP-OSD but as you see from the plot below it doesn't make much difference which order of OSD I use.