How many physical qubits does Magic state cultivation shave off from the "20 million physical qubits for RSA 2048" result?

Question

Keeping everything in How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits the same ($10^{-3}$ physical error rate, 8 hours to complete the computation, same logical algorithm e.t.c) but with the only difference being that the magic state distillation protocol is replaced with Magic state cultivation, how many physical qubits do we need to break RSA-2048?

Answer 1

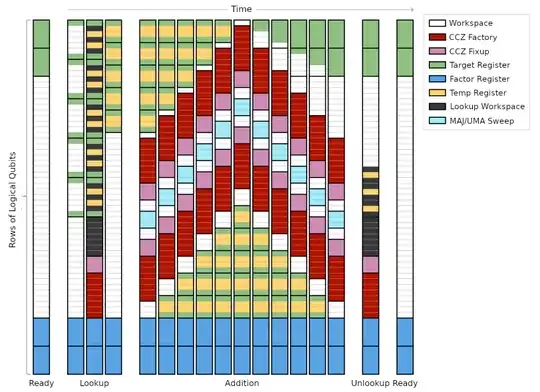
The simple answer to this question is to look at the amount of red in figure 4, and divide that part of the space by 10:

This would suggest around a 10% to 20% reduction.

The complicated answer is that when something becomes less expensive, you use more of it. So in this sense you should think of magic state cultivation as opening up design space, allowing you to pay more magic states to use less X for various X. In particular, for factoring, a major cost is the need to store such large registers. The paper you linked uses three n-qubit registers, with the third mainly being there to reduce the number of magic states required. So maybe cultivation enables switching to a two register implementation.

All that said, keep in mind an error rate of 1e-9 (cultivation with no distillation at all) isn't quite good enough here, so some distillation is still needed under the assumed gate error rate. Also, the paper "Reducing the Number of Qubits in Quantum Factoring" is far more significant here.