Qiskit Circuit Construction

Question

I have the following code block implementing $e^{-itP}$ where $P$ is a Pauli string:

import matplotlib.pyplot as plt
import qiskit
from qiskit.quantum_info import Pauli
from qiskit import QuantumCircuit
from qiskit.circuit.library import PauliEvolutionGate
from qiskit.transpiler.passes import Decompose
circuit = QuantumCircuit(3)
operator = "ZZX"
gate = Pauli(operator)
evo = PauliEvolutionGate(gate, time=1)
circuit.append(evo, range(3))
circuit.decompose().draw('mpl')

The output of the circuit is given below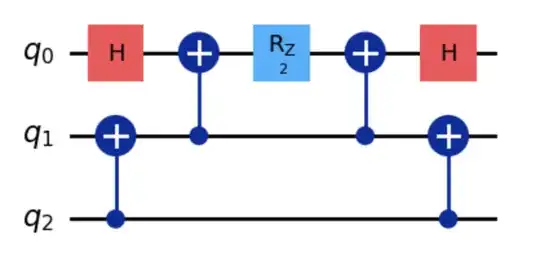

If I compare the circuit generated by Qiskit with the algorithm described this post, then, I am a bit confused. I expected Qiskit to apply the $ \sigma_z $ rotation operator on qubit $ q_2 $, followed by the CNOT gates on $ q_{0,1} $ and $ q_{1,2} $. What is happening? Is there a way to instruct Qiskit to implement the gates in the specified order?

Answer 1

Qiskit uses big-endian to order tensor products. Thus, when you write ZZX in your code, it represents the observable $Z_2Z_1X_0$, instead of $Z_0Z_1X_2$. Thus, the $\sigma_z$ rotation is indeed applied on the qubit holding the $X$ term, namely the one numbered 0.

You could apply the reverse_bits method to draw your quantum circuit and use it, but be aware that you'll have to reverse every other circuit in your code to be consistent. The quickest method is probably to remember about the way Qiskit orders tensors products.