Consider the following two quantum circuits, which are both equivalent to identity:
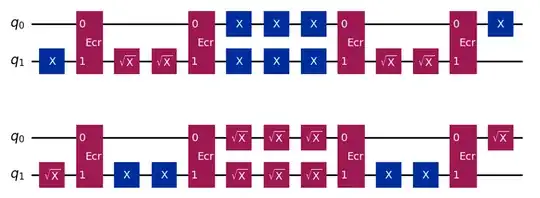
These circuits have the same structure, but the $X$ and $\sqrt{X}$ gates are swapped.
Suppose we simulate these circuits under a depolarizing noise model, with $p=0.01$ on the $\text{ECR}$ gates and $p=0.001$ on the $X$ and $\sqrt{X}$ gates, and we measure $\langle Z_0 \rangle$ (which has noiseless value $1$, since the circuits are equivalent to identity). In Qiskit, one can measure this noisy quantity exactly without the influence of shot noise, presumably by just applying the depolarizing channels after each gate. To four significant figures, the first circuit has $\langle Z_0 \rangle =0.9568$ while the second has $\langle Z_0 \rangle =0.9548$. (Full code here.)
Since these circuits have the same numbers of gates with the same error rates and the same overall function, why are their noisy expectation values different?
My thoughts:
By counting the number of gates in the lightcone of the observable (which is all of them), I would expect the noisy expectation value to be $(1-0.01)^4 \cdot (1-0.001)^{12} \approx 0.9491$. This is since each noisy gate $G$ applies a mapping $$\rho \mapsto (1-p) G \rho G^\dagger + p \frac{\mathbb{I}}{4},$$ and, inductively, the effect of $N$ gates $G_i$ with error $p_i$ is then $$\rho \mapsto \left[ (1-p_1) \cdots (1-p_N) \right] \left(G_N \cdots G_1\right) \rho (G_1^\dagger \cdots G_N^\dagger ) + \left[ 1- \left[ (1-p_1) \cdots (1-p_N) \right] \right] \frac{\mathbb{I}}{4}$$ $$=(1-0.01)^4 \cdot (1-0.001)^{12} \rho + \left(1- (1-0.01)^4 \cdot (1-0.001)^{12} \right) \frac{\mathbb{I}}{4} \equiv \tilde{\rho}$$ in our case. Then the noisy expectation value is $\text{Tr}(\tilde{\rho}Z_0) = (1-0.01)^4 \cdot (1-0.001)^{12} \approx 0.9491$. Given the results above, there must be a mistake somewhere in my argument.