Distance of the Lifted Product codes

Question

The hypergraph product code has distance determined by $\min\{d_1,d_2\}$, where $d_1,d_2$ are distances of the classical codes respectively (assuming PCM full rank). What about lifted product codes? I'm wondering if such relation also exists, e.g. distance decided by the underlying classical codes over the ring. Or even, how do I possibly get a lower bound?

Answer 1

One of the biggest misconceptions about quantum lifted product (LP) codes, unfortunately quite widespread, and I feel personal responsibility for this, is to think about them as some kind of product construction, i.e., combining two or more codes with good properties in a hope to get codes with good properties, like it happens with hypergraph product (HGP) codes. Though, formally, LP codes $\mathrm{LP}(A,B^\mathrm{T})$ are essentially just non-binary HGP codes, where the matrices $A$ and $B$ are over the ring $R=\mathbb{F_2}[G]$ instead of the field $\mathbb{F}_2$, the way this construction breaks the $\Theta(N^{1/2})$ barrier and attains linear distance $\Theta(N)$ is significantly different, and has nothing to do with the idea of combining codes of large distances (or other good properties). In fact, the main reason why we chose the name lifted product was to emphasize that it is not a traditional product construction, where you get good parameters out of the good parameters of the component codes, but rather a new general way to lift the HGP codes, or, in topological terms, construct $\ell$-fold coverings for Cartesian product of graphs.

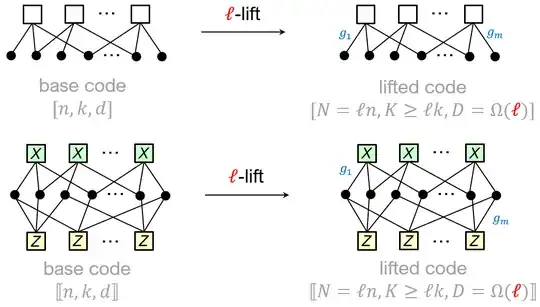
For a classical $[n,k,d]$ code defined by a Tanner graph $\mathcal{T}$, the lifted code defined by its $\ell$-lift $\mathcal{T}^{\alpha}$ has no guarantees to have a large distance; however, on average, a random $\ell$-lift does usually give you the code with the parameters $[N = \ell n, K \geqslant \ell k, D = \Omega (\color{red}{\ell})]$, provided that the permutations you assign to the edges of $\mathcal{T}$ come from a non-abelian group $G$ admitting good bounded-degree expanders (e.g., $\mathbf{S}_\ell$ or $\mathrm{PSL}(\mathbb{F}_q^t)$). LP codes are just a natural extension of this idea to higher dimensions, where instead of lifts of Tanner graphs, we use lifts of Cartesian product of Tanner graphs (i.e., lifts of HGP codes), and if we lift using a non-abelian group admitting good bounded-degree high-dimensional expanders (HDXs), then we still enjoy linear scaling of the distance (see the picture below).

Now, answering your specific question, I should say that, unfortunately, there is a very simple diagonal argument showing that LP codes are nothing like HGP codes, and there could not exist any meaningful universal lower bound for them based on the distances $d_a$ and $d_b$ of the underlying classical codes defined by the parity-check matrices $A$ and $B$, where by "meaningful" I mean beating the $\Theta(\sqrt{N})$ lower bound of HGP codes. Indeed, for $H\in R^{m\times n}$ the distance of $\mathrm{LP}(H,H^\mathrm{T})$ is always limited by $m+n$, absolutely independent of how large is the lift size $\ell=|G|$, which completely rules out any universal bound for $\mathrm{LP}(A,B)$ surpassing $\Theta(\sqrt{N})$.

However, if you are interested just in some lower bound, not necessary surpassing $\Theta(\sqrt{N})$, then, as Navneeth pointed out, at least for the subclass of LP codes called quasi-abelian LP codes in 2012.04068 (page 8), where $G$ is abelian, you have a bound coming from the Künneth theorem for modules over finite dimensional algebra $R=\mathbb{F}_2[G]$:

$$d(\mathrm{LP(A,B)}) \geqslant \frac{1}{\ell} \min\{d(\ker A), d(\ker B), d(\ker A^\mathrm{T}), d(\ker B^\mathrm{T})\},$$

which simultaneously generalizes the lower bound for HGP codes and for hyperbicycle codes (Theorem 5). Here $d(\cdot)$ denotes the minimal distance of a binary classical or quantum code. You can find the proof of the Künneth theorem for this case in the S.M. Loor thesis, which studied the subclass of quasi-abelian LP codes in great detail (in the text they are simply referred as LP codes). I wouldn't be surprised if this distance bound is also applicable to the general non-abelian LP codes such as dihedral LP codes.