is there a measurement free decoder for $[[5,1,3]]$ and $[[8,3,3]]$ codes

Question

Inspired by this post, is there a measurement free decoder for these two codes. A concrete circuit to illustrate the process would be very helpful to understand the concept.

Answer 1

I think a naive measurement free decoder can be built like this for a $[n,k]$ code:

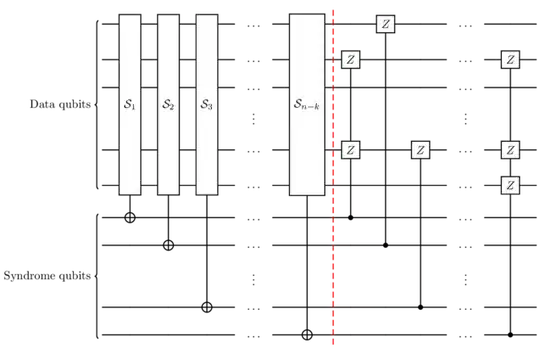
In the first part of the circuit, for each of the $n-k$ stabilizers, a syndrome qubit is entangled with the data qubits. Each $\mathcal{S}_i$ box indicates a set of controls (or Hadamard-conjugated controls) so that the measurement of the syndrome qubit would measure the stabilizer.

The second part of the circuit indicates a possible active correction of errors. Each gate corrects the error that only flip the stabilizer corresponding to the control qubit.

If you forget the dots, you get exactly the naive measurement free decoder for the $[5, 1, 3]$ code. To determine the correction, one needs to determine the destablizer operator that flips each stabilizer. The stabilizer operators of the $[5, 1, 3]$ code $\left\langle X_2Z_3Z_4X_5, X_1X_3Z_4Z_5, Z_1X_2X_4Z_5, Z_1Z_2X_3X_5\right\rangle$ are individually destabilized by (anticommuting with) $\left\langle Z_2Z_4, Z_1, Z_4,Z_2Z_4Z_5 \right\rangle$ which explain the gates used in the second part.

Note that this decoder is very bad, as it have distance 1. Indeed, a single $X$ error on the data qubits will never be corrected (since the corrections only uses $Z$ gates). So any $X$ error will induce a logical $X$ error (the correction applied will transform the $X_i$ error to $Z_2X_3Z_4$ which is the logical $X$ operator).

The destabilizers form a basis of the errors with a non-zero syndrome, but performing the correction according to the decomposition of the syndrome in this basis is not guaranteed to correct the most likely error that generates this syndrome. Some codes together with a good basis of their stabilizers might exist so that the naive decoder have a greater distance but this property is probably hard to verify.

A better decoder would implement the logic behind a look-up table for the code, where each of the $2^{n-k}-1$ possible syndromes corresponds to a $(n-k)$-controlled gate that apply the specific correction for this syndrome. Some codes might allow some factorization of this look-up table implementation (e.g. CSS codes might split the decoding in two by correcting $X$ and $Z$ errors separately), but in general such a decoder would require an exponential number of gates.