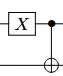
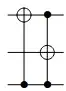
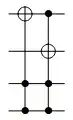
Comments
The answer appears to be yes; this gate family is in
$\mathcal{CH}$. As far as I know this is the only known gate family in
$\mathcal{CH}$ which is not semi-Clifford... though I don't think much time has been spent on the topic. The ideas I used to prove this fact seem idiosyncratic to this and very similar gate families.
Lemmas
First, I'll introduce an equivalent but nonstandard method to check membership in
$\mathcal{CH}$.
Lemma 1:
$U$ is in the $n$-qubit Clifford group iff all elements obtained by the up to 2n-fold product of distinct $UX_iU^\dagger$ and $UZ_iU^\dagger$ are in $\mathcal{CH}$ for all $i\in \{1,...n\}$. Here $X_i$ ($Z_i)$ are Pauli strings with a single qubit Pauli $X(Z)$ at location $i$ and identity gates elsewhere.
Proof: We usually demand that $U\vec{P}U^\dagger$ are in $\mathcal{CH}$ for any $n$-qubit tensor product of Pauli operators (Pauli strings) $\vec{P}$, but up to a phase ($\pm 1, \pm i$) $\vec{P}$ is a product of $X_i$s and $Z_i$s. Then, by inserting the identity we can express any $U\vec{P}U^\dagger$ as a combination of $UX_1U^\dagger UZ_1U^\dagger... UX_nU^\dagger UZ_nU^\dagger$
Lemma 2:
If $d$ is a diagonal gate in $\mathcal{CH}$, then for any permutation $P$, $PdP^\dagger \in \mathcal{CH}$.
$PdP^\dagger$ is a diagonal gate with the same entries as $d$ and since a diagonal gate is in $\mathcal{CH}$ if and only if it has entries in the ring of $2^k$ roots of unity; membership in $\mathcal{CH}$ of diagonal gates must be preserved under permutations. See here for more details.
Here's a well-known fact about the Clifford Hierarchy that I'll include for completeness.
Lemma 3:
$U \in \mathcal{CH}_k \iff C_1 U C_2 \in \mathcal{CH}_k$ for any Clifford gates $C_1$ and $C_2$.
These Lemmas are adapted from On Groups in the Qubit Clifford Hierarchy (appendix A)see arxiv:2212.05398:
Lemma 4:
For a permutation, $\pi$ and a diagonal gate $d$: $\pi \in \mathcal{CH} \mbox{ and } d \in \mathcal{CH} \implies d \pi \in \mathcal{CH}$.
The idea is that for any Pauli string, $P$, $d \pi P \pi^{-1}d^{-1} = (d \pi P_Z \pi^{-1}d^{-1}) d \pi P_X \pi^{-1}d^{-1} = D_1 (d \pi P_X \pi^{-1}d^{-1}\pi P_X \pi^{-1}) \pi P_X \pi^{-1} = D_1 D_2 \pi P_X \pi^{-1}$.
$P_X$$(P_Z)$ are the $X$$(Z)$ part of the Pauli string $P$. Since $P_Z \in \mathcal{CH}$, $\pi P_Z \pi^{-1} \in \mathcal{CH}$. and since $d \in \mathcal{CH}$ it follows that $D_1$ and $D_2$ are diagonal gates in $\mathcal{CH}$. And the term: $\pi P_X \pi^{-1}$ is individually in $\mathcal{CH}$ since $\pi$ is in $\mathcal{CH}$. If $\pi$ was in the 3rd level of the Hierarchy, we could apply Lemma 3 and be done. Otherwise, we can keep going using any choice of $P$ at each step and we will always be able to put the result in this form. Eventually, the permutation part, since it has exactly the $\mathcal{CH}$ membership constraints as $\pi$, will be Clifford and we are done.
Some details need to be filled in (see paper above), but this post is already long.
Lemma 5:
For a permutation $\pi$ it is sufficient to check that it is in $\mathcal{CH}$ for all $X$ Pauli strings.
This is basically a corollary of Lemma 4. Any $P_Z$ can be separated into its own part and it must be in $\mathcal{CH}$ since $\pi P_Z \pi^{-1}$ must be in $\mathcal{CH}$. Note that this is not necessarily enough to determine the level in $\mathcal{CH}$ of a permutation gate, but suffices to determine membership in $\mathcal{CH}$.
Proof
For our gate,
$P$, we can use Lemmas 1 and 5 to show that we need to check that all distinct (up to
$n$-fold) products of
$PX_iP^\dagger$ are in
$\mathcal{CH}$, then
$P \in \mathcal{CH}$.
In the following cases, I'll draw the circuits on only 4 qubits, but the cases $X_i$ for $i\ge 3$ are similar. All gates other than $X$ and $H$ will have controls extending down to the remaining $n-4$ qubits. Note that a diagonal gate with controls (in the computational basis) remains a diagonal gate.
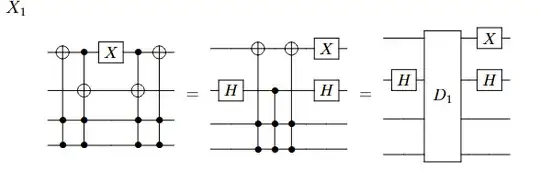
$X_2$ is trivially equal to $X_2 = H Z_2 H$.
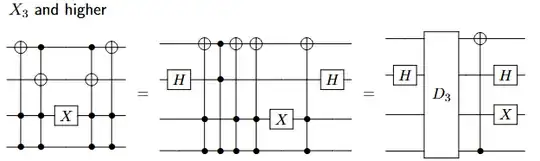
From Lemma 2 all $D_i$s in the circuits above are in $\mathcal{CH}$. Then, we can see that all the permutations remaining in the circuits above are all diagonalizable by Clifford gates (Hadamards on targets) and are therefore semi-Clifford. Note Pauli $X$s on the right side of the circuit are Clifford and by Lemma 3 do not change membership in $\mathcal{CH}$. All such diagonal matrices are in $\mathcal{CH}$ since they only have entries $\pm 1$. In fact, all semi-Clifford permutations are in $\mathcal{CH}$ as shown here.
At this point we've shown that all individual terms $UX_i U^{\dagger}$ are in $\mathcal{CH}$. We need to show that all distinct products are also in $\mathcal{CH}$.
The product of distinct $PX_iP^\dagger$ and $PX_jP^\dagger$ is
$$(PX_iP^\dagger)(PX_jP^\dagger) = H_2 D_i Q_i H_2 H_2 D_j Q_j H_2 = H_2 D_i (Q_i D_j Q_i) Q_i Q_j H_2 = H_2 D Q_i Q_j H_2.$$
By repeatedly applying the equation above we can put any distinct product of $PX_iP^\dagger$s into the form above. We will use Lemma 4 to consider the diagonal and permutation cases separately. We see that $D$ is always in $\mathcal{CH}$ by group closure of the diagonal gates in $\mathcal{CH}$. $Q_i$ are permutations including the Pauli $X$ (see right side of circuit diagrams above). For all $i$, $Q_i = Q_i^\dagger$ so we have dropped the inverse in the equation above. We can ``pull'' the Pauli $X$s to one side by toggling controls between ON on 1 and ON on 0. Then, we are left with a product of commuting multi-controlled Toffoli gates, $Q_i Q_j$. The permutation $Q_i Q_j$ is again semi-Clifford (diagonalized by Hadamard) and must be in $\mathcal{CH}$. We can proceed to look at higher order products of $UX_i U^{\dagger}$ and see that they always have this form. We conclude that the entire gate family is in $\mathcal{CH}$.
I realize a proof by induction would make the most sense here, but this is the general idea of the proof. Let me know if you find parts confusing or just plain wrong. Ideas to generalize or simplify this proof are welcome too.