I'm trying to implement a Hamiltonian simulation of a diagonal matrix explained on A.M. Childs. Quantum information processing in continuous time (Rule 1.6 in Ref. 10). Briefly, the operations are:
 $$
|a,0\rangle \rightarrow |a, d(a)\rangle
\rightarrow e^{-itd(a)}|a, d(a)\rangle \rightarrow e^{-itd(a)}|a, 0\rangle
$$
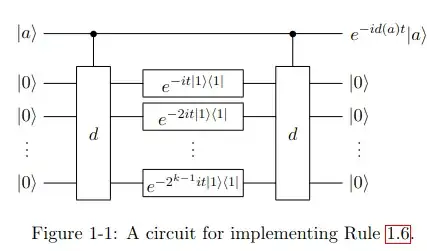
In Kothari thesis, he says that, to implement the second operation, you just have to perform a set of controlled phase gates on the first register controlled by the second register, the latter is the $ancilla$, which is coded as $h_j$.
$$
|a,0\rangle \rightarrow |a, d(a)\rangle
\rightarrow e^{-itd(a)}|a, d(a)\rangle \rightarrow e^{-itd(a)}|a, 0\rangle
$$
In Kothari thesis, he says that, to implement the second operation, you just have to perform a set of controlled phase gates on the first register controlled by the second register, the latter is the $ancilla$, which is coded as $h_j$.
My question is how implement that second operation $|a,d(a)\rangle \rightarrow e^{-itd(a)}|a, d(a)\rangle$ exactly, I can't grasp easily the way to do it.