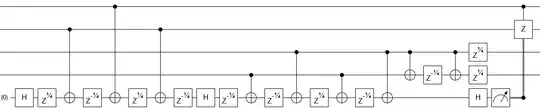
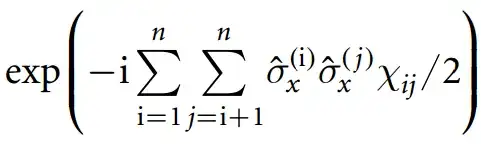(EDIT: Improved to 14 CNOTs.)
It can be done with 14 CNOTs, plus 15 single-qubit Z rotations, and no auxiliary qubits.
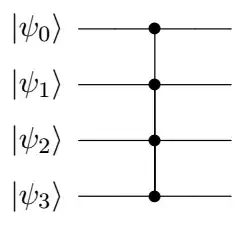
The corresponding circuit is

where the $\fbox{$\pm$}$ gates are rotations
$$
R_z(\pm\pi/16)\propto \left(\begin{matrix}1\\&e^{\pm i\pi/8}
\end{matrix}\right)
$$
Derivation:
Using the procedure described in https://arxiv.org/abs/quant-ph/03030631 , any diagonal gate - any thus in particular the CCCZ gate -- can be decomposed in terms of e.g. CNOTs and one-qubit diagonal gates, where the CNOTs can be optimized on their own following a classical optimization procedure.
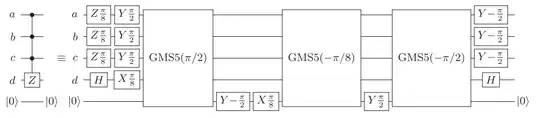
The reference provides a circuit using 16 CNOTs for arbitrary diagonal 4-qubit gates (Fig. 4).
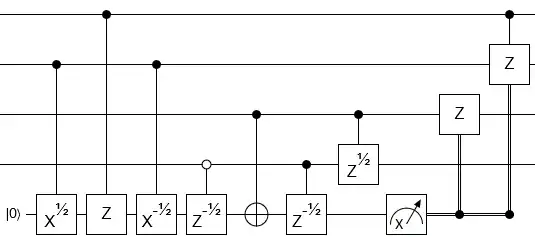
This can be improved if arbitrary pairs of qubits can be coupled to 14 qubits. For nearest neighbors with periodic (open) boundary conditions, this can be done with 16 (18) CNOTs. The corresponding circuits can be found in https://epub.uni-regensburg.de/1511/1, Fig. 5.2, 5.4, and 5.5, and can e.g. be obtained using methods to construct short Gray sequences.
The number of one-qubit gates is always 15.
Remark: While there might in principle be a simpler circuit (said circuit has been optimized with a more constrained circuit architecture in mind), it should be close to optimal -- the circuit needs to create all states of the form $\bigoplus_{i\in I}x_i$ for any non-trivial subset $I\subset\{1,2,3,4\}$, and there are 15 of those for 4 qubits.
Note also that this construction by no means needs to be optimal.
1 Note: I'm an author
 .
.