Step by step explanation of Grover diffusion operator quantum circuit for 2 qubits

Question

I am a newbie to quantum computing and recently came across Grover's algorithm. I'm now trying to understand its quantum circuit for 2 qubits.

I have understood the oracle which marks the correct answer with a negative sign. But I'm having a really hard time understanding the diffusion operator (see the image above).

I don't understand how to come up with this circuit, given the idea of reflection around the mean. I've tried to understand rotation around S and how to map it to this circuit but not able to see how.

Would someone please describe how to go from the diffusion operator's logic to creating this quantum circuit in an understandable, step by step manner? I've gone through countless articles that explain rotation around S with plenty of diagrams, operations and matrices; but none that I found explains how to convert all that to a quantum circuit, the thought process behind creating that circuit, and why that circuit works. Thanks in advance.

Answer 1

The Grover diffusion operator on 4 qubits is $$G=\frac12\begin{pmatrix}-1&1&1&1\\1&-1&1&1\\1&1&-1&1\\1&1&1&-1\end{pmatrix}=2|++\rangle\!\langle++|-I$$ with $|+\rangle$ being the uniform superposition on two qubits: $$|+\rangle=H|0\rangle=\frac{|0\rangle+|1\rangle}{\sqrt{2}}\,.$$ Using this second equation, notice what happens when you surround $G$ by Hadamard gates: $$\begin{align*} H^{\otimes2}GH^{\otimes2}&=H^{\otimes2}\left(2|++\rangle\!\langle++|-I\right)H^{\otimes2}\\&=2|00\rangle\!\langle00|-I\\&=-\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}\end{align*}\,.$$ Thus, $H^{\otimes2}GH^{\otimes2}$ is a gate that, up to an irrelavant global phase of $-1=\mathrm{e}^{\mathrm{i}\pi}$, flips the phase of the $|00\rangle$ state and leaves the other ones intact. This really looks like the $CZ$ gate, that flips only the phase of the $|11\rangle$ state.

So, in order to apply this gate, one must first flip the two qubits using an $X$ gate, and then apply the $CZ$ gate. By doing so, if the state was $|00\rangle$, it gets converted to $|11\rangle$, and the $CZ$ gate will be applied. We then mustn't forget to re-apply the $X$ gates to send back $|11\rangle$ to $|00\rangle$.

Mathematically, this is translated by: $$H^{\otimes2}GH^{\otimes2}=X^{\otimes2}CZX^{\otimes2}$$ from which we then deduce: $$G=H^{\otimes2}X^{\otimes2}CZX^{\otimes2}H^{\otimes2}$$ which is the circuit you've drawn.

More generally, the Grover diffusion operator can be written on $n$ qubits as: $$G=H^{\otimes n}X^{\otimes n}C^{n-1}ZX^{\otimes n}H^{\otimes n}$$ with $C^{n-1}Z$ being the $Z$ gate controlled on $n-1$ qubits.

---

We can check that in the $2$-qubit case, this implementation does yield the expected matrix. We have: $$\begin{align*}X^{\otimes2}H^{\otimes2}&=\begin{pmatrix}0&0&0&1\\0&0&1&0\\0&1&0&0\\1&0&0&0\end{pmatrix}\frac12\begin{pmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{pmatrix}\\&=\frac12\begin{pmatrix}1&-1&-1&1\\1&1&-1&-1\\1&-1&1&-1\\1&1&1&1\end{pmatrix}\end{align*}$$ We can now multiply by $CZ$: $$\begin{align*}CZX^{\otimes2}H^{\otimes2}&=\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\end{pmatrix}\frac12\begin{pmatrix}1&-1&-1&1\\1&1&-1&-1\\1&-1&1&-1\\1&1&1&1\end{pmatrix}\\&=\frac12\begin{pmatrix}1&-1&-1&1\\1&1&-1&-1\\1&-1&1&-1\\-1&-1&-1&-1\end{pmatrix}\end{align*}\,.$$ We now multiply with $X^{\otimes2}$: $$\begin{align*}X^{\otimes2}CZX^{\otimes2}H^{\otimes2}&=\begin{pmatrix}0&0&0&1\\0&0&1&0\\0&1&0&0\\1&0&0&0\end{pmatrix}\frac12\begin{pmatrix}1&-1&-1&1\\1&1&-1&-1\\1&-1&1&-1\\-1&-1&-1&-1\end{pmatrix}\\&=\frac12\begin{pmatrix}-1&-1&-1&-1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{pmatrix}\end{align*}$$ And finally we can multiply this by $H^{\otimes2}$: $$\begin{align*}H^{\otimes2}X^{\otimes2}CZX^{\otimes2}H^{\otimes2}&=\frac12\begin{pmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{pmatrix}\frac12\begin{pmatrix}-1&-1&-1&-1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{pmatrix}\\&=\frac14\begin{pmatrix}2&-2&-2&-2\\-2&2&-2&-2\\-2&-2&2&-2\\-2&-2&-2&2\end{pmatrix}\end{align*}$$ which is the opposite of what we were supposed to get (that is, we got $-G$). This begs two questions:

1. Why's that?
2. Why does that still work?

The first question is answered by the fact that the expression of $CZ$ is: $$\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\end{pmatrix}$$ while we were supposed to have: $$X^{\otimes2}\left(2|00\rangle\!\langle00|-I\right)X^{\otimes2}=\begin{pmatrix}-1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&1\end{pmatrix}=-CZ$$ So this is where we picked up a $-$ sign: when we applied $CZ$, it was actually the opposite of what we wanted, we should have applied $-CZ$. But as it turns out, it doesn't matter!

Indeed, this sign is what we call a global phase. That is, if instead of applying a unitary $U$, you apply $\mathrm{e}^{\mathrm{i}\theta}U$ instead, you'll always get the same results! This global phase doesn't matter, so we ignore it, which is why we can afford to have this $-1=\mathrm{e}^{\mathrm{i}\pi}$ factor while still having a functional oracle.

You can read more about the global phase here.

Answer 2

An operator U reflecting about a state $|\psi\rangle$ is given by :

$U = 2|\psi\rangle\langle\psi| - I_N. \tag{1}$
where N is the dimension of the identity vector. After a phase inversion is done by oracle the state is still in superposition, so we want to reflect about a superposition, let $|\psi\rangle$ be :

$|\psi\rangle = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle=H^{\otimes n}|0^n\rangle \tag{2}$

Puting (2) to (1) gives :
$U = 2H^{\otimes n}|0^n\rangle\langle0^n|H^{\otimes n} - I_N. \tag{3}$

Identity operator $I_N$ can be written as :
$I_N = H^{\otimes n}I_NH^{\otimes n} \tag{4}$
Putting (4) to (3) gives :
\begin{align*} U = 2H^{\otimes n}|0^n\rangle\langle0^n|H^{\otimes n} - H^{\otimes n}I_NH^{\otimes n}\\ =H^{\otimes n}(2|0^n\rangle\langle0^n-I_N)H^{\otimes n}\tag{5} \end{align*} Now we implement $2|0^n\rangle\langle0^n|-I_N$ by pauli gates, let's think about 2 qubit case for simplicity, let $U_0^\perp$ be
\begin{align*} U_0^\perp = 2|0\rangle\langle0| -I = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{pmatrix}\tag{6} \end{align*} By introducing -1 as a global phase we can rewrite (6) as follows:
\begin{align*} = -1\begin{pmatrix}-1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}=-1X^{\otimes 2}\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{pmatrix}X^{\otimes 2}\tag{7} \end{align*} Since CZ is known as : \begin{align*} CZ = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{pmatrix}\tag{8} \end{align*} (6) can be written using (7) and (8): \begin{align*} U_0^\perp = -1X^{\otimes 2}CZX^{\otimes 2}\tag{9} \end{align*} Then (9) can be written in a general form, also -1 can be ignored as it's global phase : \begin{align*} U_0^\perp = X^{\otimes n}C^{n-1}ZX^{\otimes n}\tag{10} \end{align*} Putting (10) into (5) gives :
\begin{align*} U =H^{\otimes n}X^{\otimes n}C^{n-1}ZX^{\otimes n}H^{\otimes n}\tag{11} \end{align*} (11) is what you drew in your picture.

Next, let's verify what $U$ means. $U_0^\perp$ reflects a state about $|0^n\rangle$, in other words, it flips the sign of all the basis states other than $|0^n\rangle$, the matrix can be written as : \begin{align*} U_0^\perp=\begin{pmatrix}1 & 0 & \cdots & 0\\ 0 & -1 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ 0 & 0 & \cdots & -1 \\ \end{pmatrix} \tag{12} \end{align*}

Putting (12) to (11) gives : \begin{align*} U = H^{\otimes n}\begin{pmatrix}1 & 0 & \cdots & 0\\ 0 & -1 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ 0 & 0 & \cdots & -1 \\ \end{pmatrix}H^{\otimes n} = H^{\otimes n}\left(\begin{pmatrix}2 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ 0 & 0 & \cdots & 0 \\ \end{pmatrix}-I\right)H^{\otimes n}=H^{\otimes n}\begin{pmatrix}2 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ 0 & 0 & \cdots & 0 \\ \end{pmatrix}H^{\otimes n}-H^{\otimes n}IH^{\otimes n}\\=H^{\otimes n}\begin{pmatrix}2 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ 0 & 0 & \cdots & 0 \\ \end{pmatrix}H^{\otimes n}-I=\begin{pmatrix}2/N & 2/N & \cdots & 2/N\\ 2/N & 2/N & \cdots & 2/N \\ 2/N & 2/N & \cdots & 2/N \\ \vdots & \vdots & \ddots &\vdots \\ 2/N & 2/N & \cdots & 2/N \\ \end{pmatrix}-I\\=\begin{pmatrix}2/N-1 & 2/N & \cdots & 2/N\\ 2/N & 2/N-1 & \cdots & 2/N \\ 2/N & 2/N & \cdots & 2/N \\ \vdots & \vdots & \ddots &\vdots \\ 2/N & 2/N & \cdots & 2/N-1 \\ \end{pmatrix}\tag{13} \end{align*} Let an n-qubit state $|x\rangle$ be : \begin{align*} |x\rangle = \begin{pmatrix}a_0 \\ a_1\\ \vdots \\ a_j\\ \vdots \\ a_{N-1}\end{pmatrix} \tag{14} \end{align*} Applying $U$ on $|x\rangle$ gives as follows : \begin{align*} U|x\rangle =\begin{pmatrix}2/N-1 & 2/N & \cdots & 2/N\\ 2/N & 2/N-1 & \cdots & 2/N \\ 2/N & 2/N & \cdots & 2/N \\ \vdots & \vdots & \ddots &\vdots \\ 2/N & 2/N & \cdots & 2/N-1 \\ \end{pmatrix}\begin{pmatrix}a_0 \\ a_1\\ \vdots \\ a_j\\ \vdots \\ a_{N-1}\end{pmatrix} = \begin{pmatrix}\frac{2}{N}\sum_{y=0}^{N-1}a_y-a_0 \\ \frac{2}{N}\sum_{y=0}^{N-1}a_y-a_1\\ \vdots \\ \frac{2}{N}\sum_{y=0}^{N-1}a_y-a_j\\ \vdots \\ \frac{2}{N}\sum_{y=0}^{N-1}a_y-a_{N-1}\end{pmatrix} \tag{15} \end{align*} We know $\frac{1}{N}\sum_{y=0}^{N-1}a_y = \mu(mean)$. Hence,

$\frac{2}{N}\sum_{y=0}^{N-1}a_y-a_j=2\mu - a_j \tag{16}$ (16) is nothing but inversion about the mean.

Answer 3

Great question. Here are some details to complement the answer @tristan-nemoz, and explain why the diffusion operator works in the first place.

As you correctly stated, the job of the diffusion operator is to "reflect" the probability amplitudes about the mean. So, in the case of two qubits ($n = 2$), this is how Grover's algorithm will go:

1. Place qubits in equal superposition:

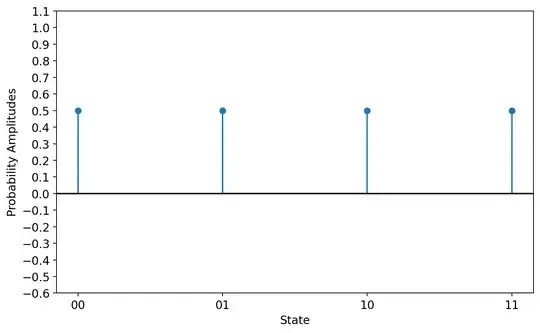
$$ \begin{aligned} |\psi_1\rangle &= \frac{1}{\sqrt{2^n}} \sum_{i = 0}^{2^n} |i\rangle \\ \\ &= \frac{1}{2}\left(|00\rangle + |01\rangle + |10\rangle + |11\rangle\right) \end{aligned} $$

If we graph the probability amplitudes for each state, it will look like this:

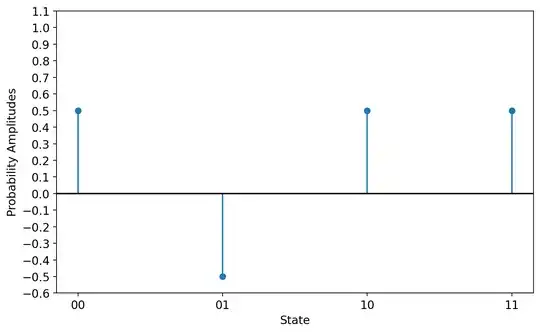
2. Apply the oracle $U_f$ to "flip" the probability amplitude of the marked element (since you mentioned you know how this works and how to construct the circuit, I won't go into details). For argument sake, let's assume the marked state is $|01\rangle$:

$$ |\psi_2\rangle = \frac{1}{2}\left(|00\rangle - |01\rangle + |10\rangle + |11\rangle\right) $$

3. "Flip" all probability amplitudes $\alpha_i$ about the mean. So, for this, we need to compute the mean $\mu$, which is easily done by adding all probability amplitudes and dividing by the total number of elements ($2^n$):

$$ \begin{aligned} \mu &= \frac{1}{2^n}\sum_{i = 0}^{2^n} \alpha_i \\ \\ &= \frac{1}{4}\left(\frac{1}{2} - \frac{1}{2} + \frac{1}{2} + \frac{1}{2}\right) = \frac{1}{4} \end{aligned} $$

Notice that the distance between the current probability amplitudes $\alpha_i$ and the mean $\mu$ is simply $\alpha_i - \mu$, which pictorially looks like this:

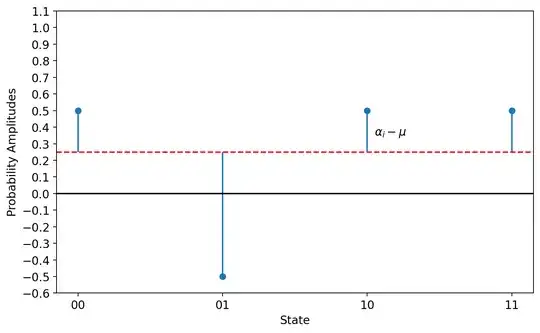
It is important to note that in the fig above we haven't changed anything with respect to step 2, we're just redrawing the amplitudes starting from the mean.

Now, after the reflection about the mean, the graph will look like this instead:

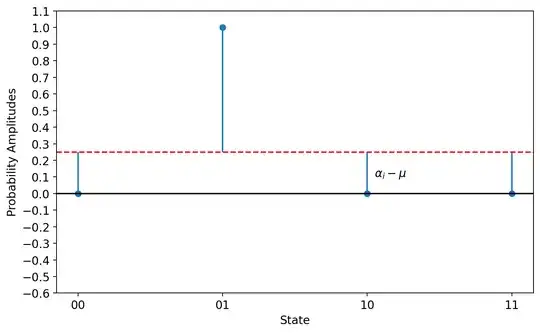
The distance between each probability amplitude to the mean will still be $\alpha_i - \mu$, but now they will go in opposite direction. So the question is, what is the new value of each probability amplitude? (i.e., what is the distance from the $0$ line to the new $\alpha_i$?). Well, in general, that would be the distance from $0$ to the mean line minus the distance from the mean line to the amplitude $\alpha_i - \mu$, so we have:

$$ \begin{aligned} \alpha_i^{(new)} &= \mu - (\alpha_i^{(old)} - \mu) \\ \\\alpha_i^{(new)} &= 2\mu - \alpha_i^{(old)}, \end{aligned} $$

where $\alpha_i^{(old)}$ and $\alpha_i^{(new)}$ are each of the prob amplitudes before and after the reflection about the mean, respectively.

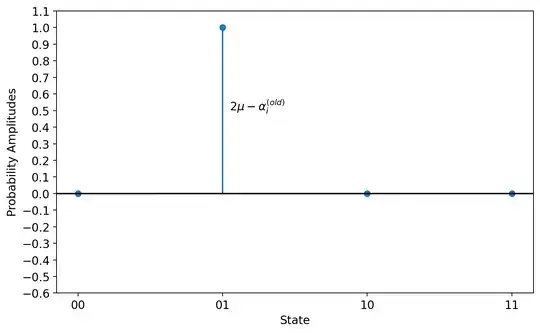
So, the column vector with all new probability amplitudes is given by:

$$ \begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(new)} = 2\mu - \begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(old)}.$$

One thing to note is that, one can compute the mean of a column vector by taking the inner product of that vector with an "all ones" row vector:

$$\mu = \frac{1}{2^n}\begin{bmatrix}1 & 1 & \dots & 1 \end{bmatrix} \begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix} = \frac{1}{2^n}(\alpha_0 + \alpha_1 + \dots + \alpha_{2^n-1})$$

You can replace the expression for the mean in for each new probability amplitude by turning it into a matrix:

$$ \begin{aligned} \begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(new)} = 2\frac{1}{2^n}\begin{bmatrix} 1 & 1 & \dots & 1 \\ 1 & 1 & \dots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \dots & 1 \end{bmatrix}\begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(old)} - \begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(old)}. \end{aligned} $$

Then, we can factorize the old prob amp vector to find what is the unitary $U_s$ needed to find the new prob amp vector (which are the matrices inside the parenthesis):

$$ \begin{aligned} \begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(new)} = \left(\underbrace{\frac{2}{2^n}\begin{bmatrix} 1 & 1 & \dots & 1 \\ 1 & 1 & \dots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \dots & 1 \end{bmatrix}}_{2| s \rangle \langle s |} - \underbrace{\begin{bmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{bmatrix}}_I \right)\begin{bmatrix}\alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{bmatrix}^{(old)}. \end{aligned} $$

where $|s\rangle$ is the equal superposition state and $I$ the identity matrix. So we have:

$$ U_s = 2| s \rangle \langle s | - I .$$

To generate the equal superposition state, one takes the all-zeros state and apply a Hadamard to each qubit: $| s \rangle = H^{\otimes n}| 0 \rangle^{\otimes n}$.

So, replacing $|s\rangle$ (and $\langle s |$) in the operator expression, you get:

$$ U_s = 2 \, H |0\rangle \langle 0| H - I,$$

where I have omitted the $^{\otimes n}$ superscript for the $H$ gates (and all-zeros state) for convenience.

Now, since $HH = I$, we can sandwich the identity in the expression above without changing the result:

$$ \begin{aligned} U_s &= 2 \, H |0\rangle \langle 0| H - H \, I \, H \\ \\ U_s &= H \left ( 2 |0\rangle \langle 0| - I \right) H \end{aligned} $$

Next, consider the matrix representation of the expression in between the $H$ gates above:

$$ \begin{aligned} 2 |0\rangle \langle 0| - I = & \, \begin{bmatrix} 2 & 0 & \dots & 0 \\ 0 & 0 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 0 \end{bmatrix} - \begin{bmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{bmatrix} \\ \\ 2 |0\rangle \langle 0| - I = -1 & \, \begin{bmatrix} -1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{bmatrix} \end{aligned} $$

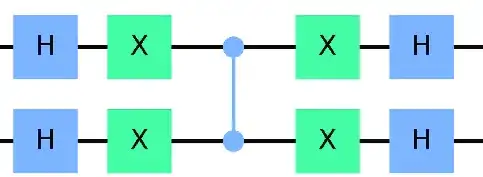
This last matrix corresponds to a gate that inverts the phase of the all-zeros state, and the pre-factor of $−1$ is simply associated with a global phase we can ignore. To construct this gate, you can first flip all bits with an $X$ gate, apply a multi-controlled $Z$ gate on all qubits $\text{MC}Z$, and then flip the bits back with another $X$:

$$2 |0\rangle \langle 0| - I = X \, \text{MC}Z \, X .$$

Replacing in $U_s$, you get the following sequence of gates: $$U_s = H \, X \, \text{MC}Z \, X \, H,$$

where, again, all of these are being applied to all qubits. And this expression is exactly the circuit you have in your diagram.