Why can't "oblivious carry runways" be fully removed from Gidney's implementation of Shor's algorithm?

Question

Hoping that @CraigGidney can hop in here.

I'm trying to understand oblivious carry runways and how it interplays with the rest of the windowed arithmetic implementation of Shor's algorithm as presented in "How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits" (arxiv:1905.09749).

Specifically, why can't we just remove the runways entirely when a register is needed as the input into the lookup addition? I think this isn't explain very well in his paper.

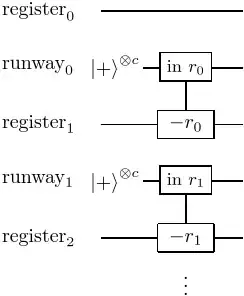
My understanding is that the runways are initialized like this:

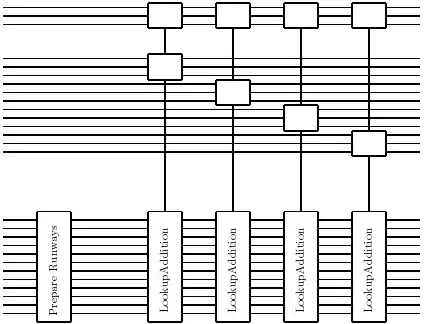
A sequence of LookupAdditions are then implemented that add values into this register, where the additions on each segment are performed in parallel and each segment carries into the subsequent runway.

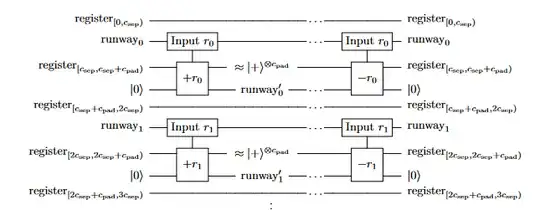
When this register then needs to be used as inputs for the next sequence of LookupAdditions, I understand that the extra runway qubits increase the total number of qubits in the register, thus increasing the number of windows that must be iterated over. But in his paper, Gidney says that the runway can be "reduced to a single qubit" like this:

What I don't understand is this line in the paper:

We could reduce the runways to zero qubits, but this would require propagating the carry qubits all the way across the register, so we do not.

Why would it mean that we have to "propagate the carry qubits all the way across the register"?

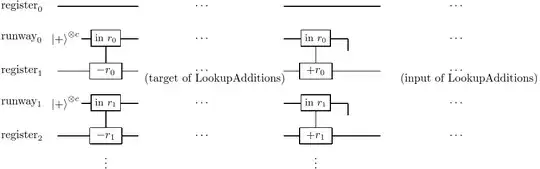
Why can't we simply perform the reverse of the runway preparation, something like this, where the runways are removed entirely?

I've looked through this paper on "Approximate encoded permutations and piecewise quantum adders" (arxiv:1905.08488) where it explains in more detail how the runways work. If you have a permutation $u$ of unencoded values, a permutation $v$ of encoded values, and a reversible encoding function $f$, this is a good "approximate encoded permutation" if (roughly) $$ f^{-1} \circ v \circ f \approx u. $$ In the case of the piecewise adder, the encoding function is exactly the operation of adding runways as shown in the first image in this question (1). So why can't we just perform the inverse of the encoding when we are done with the piecewise additions?

This paper (arxiv:2105.01533) also has a section on how oblivious carry runways interact with the rest of the algorithm, but those authors needed to

fully propagate and decode the runways into the registers before using them as inputs into multiplications

because they were creating circuits for much smaller RSA numbers and the runways were about as large as the segments. However, I still don't quite understand why the runways need to be "fully propagated" and would appreciate an explanation!

Answer 1

Your initialization circuit is incorrect. The subtraction of $r_0$ out of part 1 of the register needs to actually subtract $r_0$ out of the concatenation of the entire register starting where part 1 starts. The subtraction needs to carry from part 1 into part 2. Otherwise the system won't maintain the property that the sum of the register and the runways is equal to 0 (or more generally the represented value).

For example, consider what happens to the part of the superposition where the runway is storing $1$ during initialization. The runway is at bit offset $k$, so this 1 is worth $2^k$. So the register must end up storing $-2^k = 2^n - 2^k$ to compensate for this extra $2^k$. If you cut off the subtraction early then you'll end up with the register storing $2^k + 2^{k+1} + \dots + 2^{c-1}$ for $c < n$, instead of $2^n - 2^k$, and so the represented value won't be zero.