Here is a simple circuit that produces a superposition proportional to a sine envelope $\sum_{k=0}^{n-1} \sin(\pi k/n)$:
Is there also a simple circuit to prepare a 1-cosine envelope? A state proportional to $\sum_{k=0}^{n-1} 1 - \cos(2\pi k/n)$.
Note this is a different state. In particular, the 1-cosine envelope lacks the slope discontinuity that the sine envelope has:
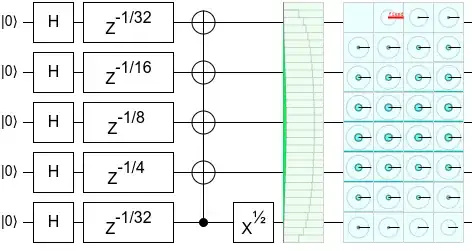
One way to achieve this is to use Fourier state loading, that is by utilizing the fact that QFTs map from the frequency domain to the space domain.
As you've already shown in your example the state
(in the below maths I drop all normalization constants)
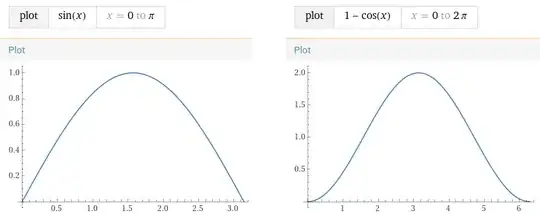
$$|\psi\rangle = \sum_i^N \sin(2\pi i k/N) |i\rangle$$
is dual to
$$QFT | \psi \rangle = |k\rangle + |N-k\rangle$$
In the same vein,
$$|\psi\rangle = \sum_i^N 1-\cos(2\pi i k/N) |i\rangle$$
is dual to,
$$QFT | \psi \rangle = |0\rangle -|k\rangle - |N-k\rangle$$
The problem then reduces to finding any circuit that loads a superposition like this a good solution is given here
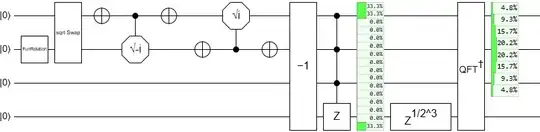quirk link
It’s worth noting that FSL algorithms are always at least $\mathcal{O}(log(N)^2)$ because of the QFT, so in principle it should be ok for most stuff, hope this answers your question :-)
Here is a fixed version of Billy's answer, with a circuit that correctly produces the 1-cos envelope:
The "2:1" gate in the diagram is an $R_Y(\theta)$ gate tuned to perform $|0\rangle \rightarrow \sqrt{\frac{2}{3}}|0\rangle + \sqrt{\frac{1}{3}}|1\rangle$.
The idea is to make a cosine envelope via $\cos(t) \propto e^{1 \cdot it} + e^{-1 \cdot it}$, and offset it with a DC term $e^{0 \cdot it}$ to get the "1-". Concretely: prepare a state of the form $a|0\rangle + b\sqrt{\frac{1}{2}}(|1\rangle + |-1\rangle)$ and then apply a QFT. It turns out you want a 2:1 ratio between the squared magnitudes of $a$ and $b$, with $b$ being negative and $a$ being positive, which you can figure out by solving for the requirement that the output amplitude of $|0\rangle$ must be 0 and all other amplitudes must be positive real numbers.