The Towers of Hanoi is an old puzzle that involves moving $n$ discs of different radii among $k$ pegs, requiring each stack of discs to be monotonically increasing along the stack. Conventionally $n=6$ or so and $k=3$; it's also often studied in introductory algorithms classes, as it has a nice recursive algorithm and necessarily requires an exponential number of moves to move all the discs to a different tower, (hence, splitting P from EXP).
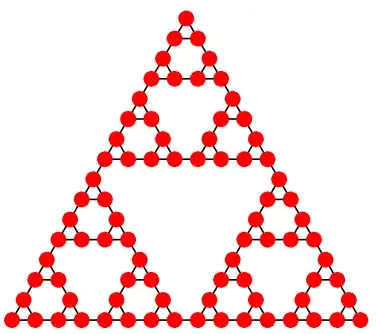
Nonetheless I think we can get a quantum algorithm for the puzzle by judiciously performing partial SWAPs between the topmost disc of one peg and a blank (NULL) disc of another; indeed, reviewing the graphs of the state space, I think we can pretty easily edge-color the moves from disc 1 to disc 2 separately from those between disc 2 to disc 3, and disc 1 to disc 3. A four-disc graph from MathWorld is clipped below (all the discs are on one peg at each of the vertices of the main triangle).
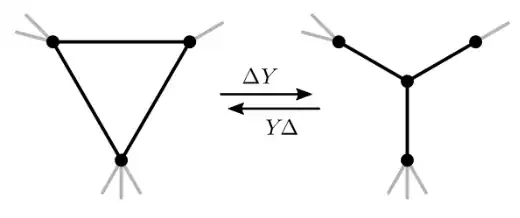
Additionally, as noted by Alekseyev and Berger's study of classical random walks on the graph, we can borrow some ideas from electrical engineering and iteratively perform a delta-wye transform on each of the triangles; this transform leaves invariant pertinent properties of the spectrum of the graph, and I think much as the welded-trees is seen by a quantum particle as merely a "path graph," the Hanoi graph will be seen similarly as three long paths connected in a Y-shaped star $S_3$.
To that end, I suspect a quantum walk could potentially get at least a Grover-like speed-up over the exponential time outlined in Alekseyev and Berger, but I'm also interested as to how much interference actually happens in the middle of the Y.
For example, labeling the states with all the discs on the left, middle, and right pegs as $|L\rangle, |M\rangle, |R\rangle$, could we get perfect state transfer between $|M\rangle$ and $\frac{1}{\sqrt 2}\left(|L\rangle+|R\rangle\right)$? Even if it takes time that's exponential in the number of discs $n$?