I learned from Aaronson's blog about a recent preprint by Jordan, Shutty, Wootters, (our very own) Zalcman, Schmidhuber, King, Isakov, and Babbush that provides an efficient quantum algorithm to give good solutions to what they call the "optimal polynomial intersection" problem.
OPI: Given integers $n$ and $p$ with $n<p$ and $p$ prime, and also given as input subsets $F_1,\cdots, F_{p-1}$ of the finite field $\mathbb F_p$, find a degree-$(n-1)$ polynomial $Q$ that maximizes the number of $y\in\{1,\cdots,p-1\}$ such that $Q(y)\in F_y$, i.e. that intersects as many of the subsets as possible.
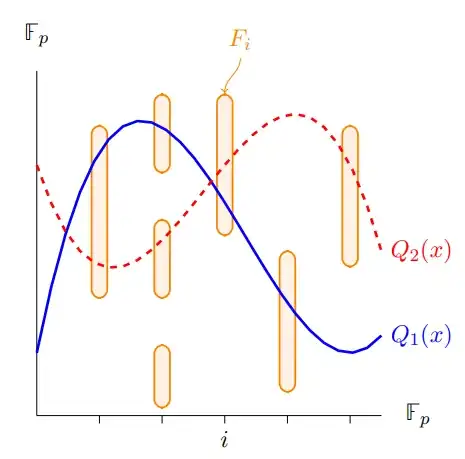
It took me some time to grasp even the point of the problem - but Figure 1 of their paper is very nice. Briefly we're looking for a low-degree polynomial $Q$ that can touch as many vertical subsets $F_y$ as possible. The solid blue curve $Q_1$ could try to swing up to intersect the rightmost subset $F_i$, or the dashed red curve $Q_2$ could swing down and intersect the second-to-right subset $F_i$, but doing either requires increasing the degree of the respective polynomials.
Of course we're working in the finite (discrete) fields $\mathbb F_p$ so 'swinging up' and 'swinging down' don't really mean what they would mean if we were working in (say) $\mathbb R$. However Figure 1 is also quite suggestive that there could be somewhat practical applications to such an algorithm - even if a bit contrived. Is there an obvious practically relevant instantiation of the OPI problem? For example spline-fitting or robotics control or data compression or telemetry or ...?
Jordan et al.'s algorithm has some similarities to Yamakawa and Zhandry's earlier "Verifiable Quantum Advantage Without Structure" (arXiv, ACM), but it's being applied to an NP-optimization problem rather than the NP-search problem considered by Yamakawa and Zhandry. Further the paper has been compared and contrasted with the Quantum Approximate Optimization Algorithm (QAOA) - which also works on NPO problems.