4

I'm following this toric code tutorial, where they constructed the $X$-logicals matrix using the Künneth theorem.

I'm confused about why they specifically used $X$-logicals when only $Z$ errors were allowed to occur.

I used the following code to create the $Z$-logicals matrix manually.

def toric_code_z_logicals(L):
    n_qubits = 2 * L * L  # Total number of qubits in the toric code lattice
    matrix = dok_matrix((2, n_qubits), dtype=int)  # Two logical Z operators

# Logical Z Operator 1: Mark every L-th qubit starting from the first qubit
logical1_indices = [i * L for i in range(L)]

# Logical Z Operator 2: Mark all qubits in the last row of the lattice
logical2_start = n_qubits - L  # Starting index of the last row
logical2_indices = [logical2_start + i for i in range(L)]

# Fill in the matrix for the two logical Z operators
for idx in logical1_indices:
    matrix[0, idx] = 1
for idx in logical2_indices:
    matrix[1, idx] = 1

return matrix.todense()

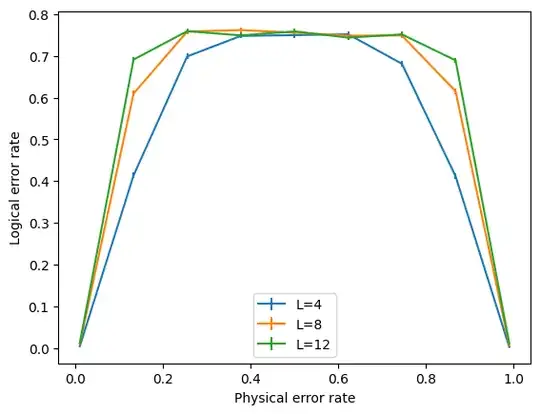
I tried using $Z$-logicals instead but ended up with the following graph that looks like a bell curve when plotting the physical vs logical error graph using physical errors up to one. enter image description here

FDGod
  • 2,901
  • 2
  • 6
  • 31
Rahul Dev Sharma
  • 47
  • 4

1 Answers1

1

I do not think this graph is a bell curve, but a parabola. Most specifically, I suspect it is very close to the probability of errors of two random binary variable under flip noise.

Indeed, if $A$ and $B$ are two random binray variables that are flipped with probability $p$, the probability of either being flipped is $2p-p^2$ for $p\leq0.5$ and is $2(1-p)-(1-p)^2$ for $p \geq 0.5$ which peaks at $0.75$ for $p=0.5$ and has value $0$ for $p=0$ and $p=1$.

If $A$ and $B$ are instead the random events "an odd number of flips happened on repetition code $A$ or $B$", this would explain the slightly worsening curves with increasing $L$.

Ranges of $p$ traditionally studied are $[10^{-3}, 10^{-1}]$ or below, because above some value coined the threshold, having a higher $L$ is detrimental (and the code is useless). You have no data point in this range, so it is hard to tell if something is wrong here.

Homever, you seem confused about the relation between errors and logical operators. If you look at $X$ logical operators, this means you will eventually measure your logical state in the basis $\{|+\rangle_L, |-\rangle_L\}$, so your goal is to avoid that a random $Z$ logical operator occurs due to noise. Such an operator can only occur when some $Z$-errors happen in the code.

To detect these $Z$-errors, you measure the $X$-stabilizers (aka the $X$ parity check matrix) because these are the stabilizers that will be flipped by these $Z$ errors (the $Z$-stabilizers will commute with these errors so they won't be flipped).

Hence, merely changing $X$ to $Z$ logical operators is wrong, you have to change from using $X$ to using $Z$ stabilizers too, because it is the $X$ errors that you now care about. If you do not do that, you will still account for $Z$-errors with your syndrome decoding, but under the simplest error model this would not help you at all correct $Z$ logical errors.

Said differently, the logicals you list in an experiment are not some representatives of the logical errors you want to avoid, but some representatives of the logical observables you want to protect.

AG47
  • 1,575
  • 3
  • 16