I've been going through various papers on MBQC for a while now, and I am still not clear on how we perform gates on 2D cluster states. On 1D clusters it's very clear, just a series of measurements in either the $X$ or a rotated basis $\{|0\rangle + |1\rangle, |0\rangle +e^{-i\theta} |1\rangle \}$. Each measurements generates $Z^{m}HU$, where $U^{\dagger}XU$ generates the rotated basis. Due to the by-product operators$$U_{Z}(\theta)\to U_{Z}(\theta(-1)^{m})\,,$$ due to the propogation of by-product operators to the end of the circuit. This leads to measurement adaptivity, ie alteration of the sign of the measurement basis after we get a measurement outcome so that it will still implement the transformation we want.
However, I am having trouble on how these by-product operators come about, and the teleportation of the state, when we move to 2D clusters. In general, I cannot find concrete sources or examples of how 2 qubit gates are actually implemented, and why it works, An example I am looking at, but having issue with, is the following representation of a CNOT gate on a 4 qubit cluster:
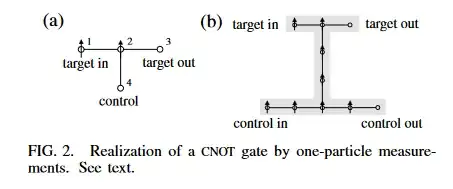
Specifically figure 2.(a) in A One-Way Quantum Computer. They state that the end state should be $$|s_{1}\rangle_{x,1}\otimes|s_{2}\rangle_{x,2}\otimes U_{\Sigma}^{34}(|i_{4}\rangle_{z,4}\otimes|(i_{1}+i_{4}) mod 2\rangle_{z,3})$$ with $$U_{\Sigma}^{34}=\sigma_{z}^{3^{s1+1}}\sigma_{x}^{3^{s2}}\sigma_{z}^{4^{s1}}$$
Now maybe I have missed something obvious in the literature, but it's not clear to me how they are arriving at this. Given a starting state of, for example, $$|0\rangle_{z,1}\otimes|1\rangle_{z,4}\otimes|+\rangle_{x,2}\otimes|+\rangle_{x,3}\,,$$ after performing the $CZ$ operations between 1 and 2, 2 and 3 and 2 and 4, and measuring 1 and 2, after measuring the readout, ie 3 and 4, and reordering them gives $$|-\rangle_{x,1}\otimes|-\rangle_{x,2}\otimes|0\rangle_{x,3}\otimes |1\rangle_{z,4}$$ with
$$U_{\Sigma}^{34}=\sigma_{x}^{3}\sigma_{z}^{4}$$
which means, discounting $U_{\Sigma}^{34}$, I have $|-\rangle_{x,1}\otimes|-\rangle_{x,2}\otimes|1\rangle_{x,3}\otimes |1\rangle_{z,4}$, which is the desired outcome of flipping qubit 1 based on qubit 4 being $|1 \rangle$.
What I would like to understand is how the byproduct operators emerge as a result of the measurements., ie where Z and H emerge from. I feel like most of the literature on MBQC really does ignore higher dimensional clusters despite their importance w.r.t examples, with few solid ones of how 2d is meant to work. Most of it focuses on eigenvalue and stabilizer formalism, but as I havent't work with computations in this manner, I am unsure how it progresses.
Edit: Taking a look at Measurement-based quantum computation with cluster states, the general method is to update the eigenvalue equations or the stabilizers with commuting stabilisers given the measurements. But what is not clear to me is how we can take the starting set of stabilizers for the cluster state, and get the end by-product operations from them. These are the starting stabilizers, but the usual process of taking the anti-commuting ones and taking their product, and introducing the new stabilizer doesn't work here, as we have measurement results. Additionally, it isn't clear how the bi-product operators emerge from this.
$$\{ \sigma_{x}^{1}\sigma_{z}^{2},\sigma_{x}^{4}\sigma_{z}^{2},\sigma_{x}^{3}\sigma_{z}^{2},\sigma_{x}^{2}\sigma_{z}^{1}\sigma_{z}^{3}\sigma_{z}^{4} \}$$ Th