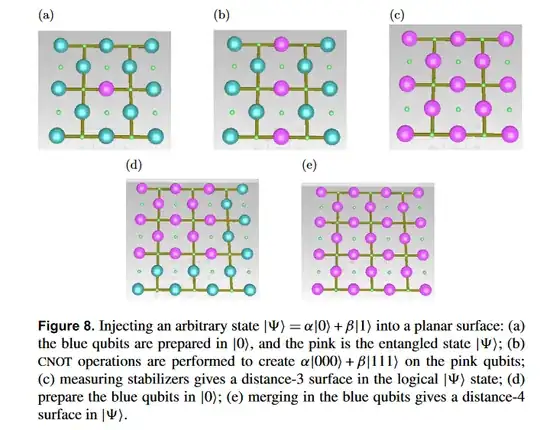
Looking at the oringal paper on lattice surgery on the surface code, the expansion step of the state injection process is meant to take $$\alpha|0\rangle_{L}+\beta|1\rangle_{L}$$ to a larger surface code patch. However, both this question and this one seem to indicate that the expansion process doesn't work, or has issues.
The main issues seem to be with the two bottom figures, and the fact that all the data qubits are initialised in $|0\rangle$. Looking at figure d, the merge process involves both a smooth and rough merge. This means that on the right hand side, you are rough merging and measuring $X_{L}X_{L}$ on both surfaces, effectively putting them into an + or - eigenstate of $X_{L}X_{L}$, depending on the outcomes. But for the bottom row, it's a smooth merge, and the qubits are initialised to the wrong states for that to occur. They'd need to be in $|+\rangle$.
Additionally, as pointed out in 2, the smooth merge would be measuring $Z_{L}Z_{L}$, and the parity of the bottom row qubits, one $Z_{L}$, and the original 3 qubit one plus an additional one from the right hand side of the lattice, giving the $Z_{L}$ for the pink surface, would have to match the parity of the 4 face stabilisers at the bottom. But this would only match for the surface being initialised in either the logical 0 or 1. ie if it was a superposition, wouldn't the expansion destroy the injected state? The green surface is already a +1 eigenstate of $Z_{L}$, so shouldn't this remain the case after the measurements?