Imagine a database of DNA fingerprints, each one characteristic of only one person. You are given a DNA trace and asked to find the person to which it belongs. There is no way (to my knowledge !) to sort DNA fingerprints so that you are left to compare each DNA fingerprint of the database with your particular trace.
Given the size of such genetic database, this is where the Grover's algorithm may come in handy. Grover's algorithm is based on an Oracle function which links the quantum algorithm itself to the database and its queries.
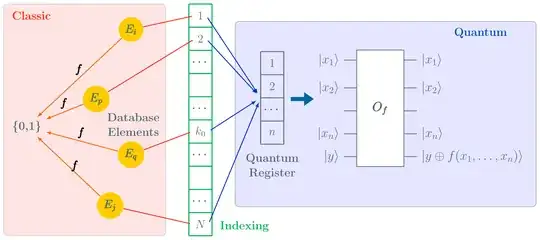
Following figure is an attempt to represent the Grover's algorithm, definitely lying on the Quantum side, with respect to the database itself, which lies in the Classic world. In between is the database elements indexing, each element of the database is assigned an index, regardless of its inner position in the database. Each index is encoded in the quantum register.
On the Classic side, you can build a function $f$ with your particular DNA trace $T$, which takes in input a database element $E$, and returns $1$ if $T$ and $E$ are identical, i.e. belonging to the same person, or $0$ otherwise.
Oracle $O_{f}$ performs the evolution :
\begin{equation} |y\rangle = |- \rangle \quad,\quad O_{f}(|\psi_{H}\rangle \otimes|y\rangle) = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1}|k\rangle \otimes|y \oplus f(k) \rangle = \dots = \biggl(\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}(-1)^{f(k)}|k\rangle \biggr)\otimes|- \rangle \end{equation}
which means that previous function $f$ is applied to each fundamental state of the superimposed state $|\psi_{H}\rangle$. But then, this means we would have to call the classic function $f$ for all indices and consequently for all database elements, which would make useless the quantum algorithm ?
How do you concretely implements the oracle in such real life use cases ?