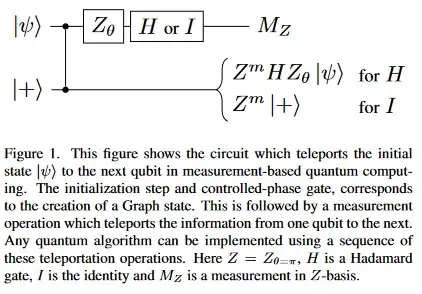
I'm looking at Lattice Surgery on the Raussendorf Lattice, and I am getting confused by one of their teleportation circuits.
In Figure 1, they show the following circuit to achieve MBQC:
It differs from ordinary MBQC circuits in that they measure in the $Z$ basis, as opposed to the X. But one can easily see that this is the same as measuring in the $X$ basis due to the $H$ gate they apply just before measurement, which can be commuted to the end of the circuit, and performs a measurement in the $X$ basis instead. If this is done, it is just the ordinary MBQC circuit.
However the operation they perform on the teleported qubit seems to be wrong. A straightforward calculation shows that:
$$HZ_{\theta}C_{Z}|\psi\rangle\otimes|+\rangle=HZ_{\theta}(\alpha|0\rangle\otimes|+\rangle+\beta|1\rangle\otimes|-\rangle)=H(\alpha|0\rangle\otimes|+\rangle+\beta e^{i\theta}|1\rangle\otimes|-\rangle)\\ =\alpha|+\rangle\otimes|+\rangle+\beta e^{i\theta}|-\rangle\otimes|-\rangle$$
From here, measuring the first qubit in the $Z$ basis, and ignoring normalisation for the moment, will give $$|0\rangle \otimes \alpha|+\rangle+\beta e^{i\theta}|-\rangle$$
or
$$|1\rangle \otimes \alpha|+\rangle-\beta e^{i\theta}|-\rangle$$
In the first case, when the measurement outcome is +1, you can see this is $|0\rangle \otimes HZ_{\theta}(\alpha|0\rangle+\beta |1\rangle)$, and the byproduct operator has no effect. However, in the case of -1, you don't get $ZHZ_{\theta}|\psi\rangle$, as $$|1\rangle \otimes \alpha|+\rangle-\beta e^{i\theta}|-\rangle=|1\rangle \otimes XHZ_{\theta}(\alpha|0\rangle+\beta |1\rangle)$$
All the byproduct operator $Z^{m}$ would do, if included, is flip the bits.
So what am I missing here? Am I wrong or is this a mistake in the paper? I'll also point out that the equivalent action of measuring in the $X$ basis instead, which, up to a certain operation, would give the same, does give a $Z$ byproduct operator, but before the hadamard, which when rearranged achieves the same operation as the one I arrive at.
Shouldn't it be $$|1\rangle \otimes X^{m}HZ_{\theta}(\alpha|0\rangle+\beta |1\rangle)$$ or, in the original MBQC circuit, $$|1\rangle \otimes HZ^{m}Z_{\theta}(\alpha|0\rangle+\beta |1\rangle)$$