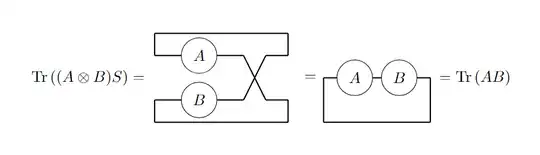
I'm trying to prove $P(\rho)={\rm tr}((\rho \otimes \rho')S)$, where $P(\rho)={\rm tr}(\rho^2)$ is the purity and $S$ is the swap operator. My question is that since ${\rm tr}(AB)={\rm tr}(BA)$, do we have $${\rm tr}((\rho \otimes \rho')S)={\rm tr}(S(\rho \otimes \rho'))={\rm tr}(\rho' \otimes \rho)={\rm tr}(\rho'){\rm tr}(\rho)\,?$$
However, I just cannot get a result that matches ${\rm tr}(\rho^2)$ by expanding $\rho$ in ${\rm tr}((\rho \otimes \rho')S)$ or ${\rm tr}(\rho'){\rm tr}(\rho)$.
In fact, we have a more general equality: $$ {\text Tr}(AB) = {\text Tr}((A\otimes B) S), $$ for any square matrices $A,B$.
If $A = |a\rangle\langle b|$ and $B = |c\rangle\langle d|$ then $$ {\text Tr}(AB) = \langle b|c \rangle\langle d|a \rangle $$ and $$ {\text Tr}((A\otimes B) S) = {\text Tr}(|a\rangle\langle d| \otimes |c\rangle\langle b|) = \langle d|a \rangle\langle b|c \rangle, $$ so they match. But both sides are linear in $A$ and $B$ hence the equality is true for any $A,B$.
You can easily prove that identity using graphical notation that depicts tensor contractions by lines:
EDIT: It seems like the graphical notation is less known than I anticipated. Doesn't matter. The above equation also has an index form $${\rm Tr}\left( (A \otimes B) S \right) = A^a_b B^c_d S_{ac}^{bd} = A^a_b B^c_d \delta_a^d \delta^b_c = A^a_b B^b_a = {\rm Tr}\left( AB \right), $$ where I used the $S^{bd}_{ac} = \delta_a^d \delta_c^b$ to write the elements of the SWAP operator and Einstein's summation convention indicating summation over double indices.
