Understanding errors in rotated surface code magic state injection

Question

I am going over this paper by Lao, and I am trying to understand how they count the two-qubit errors that induce logical errors.

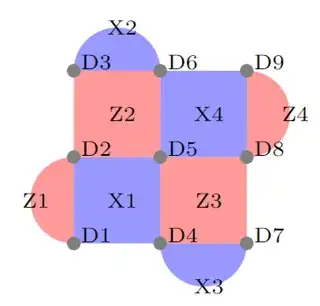
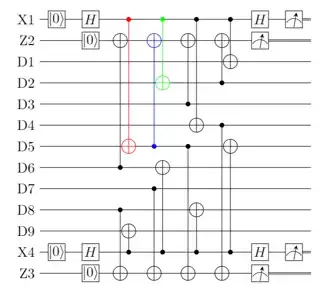
I am looking at the middle-type injection, which looks like this:

Now, they count which two-qubit errors change the logical operators. I understand I can do it by one of two methods:

1. The first is by propagating each possible error to the beginning of the circuit and checking whether it changes the value of the logical operators at that point. For example, $\color{blue}{X_c X_t}$ error on the blue CNOT will propagate to be an $X_5$ error, which changes the injected qubit state.
2. The second is propagating the error to the end of the circuit and checking whether it will be detected on the next cycle. Here, the $\color{blue}{X_c X_t}$ error will propagate to flip both $Z_2$ and $Z_3$ stabilizers and also $X$ error on D5. This will not be corrected on the next circuit because no stabilizers will be flipped.

I tried to do it for some errors and failed to understand, for example, the error $\color{red} {I_c Z_t}$ on the red gate which they do not count as an undetectable logical error:

• when propagated to the start it becomes $Z$ error on D5 and flips stabilizer X1. Why is this not changing the value of the logical operator? Or maybe it is detected and discarded? If so, how is it detected, considering X1 is not deterministic?
• when propagated to the end, it becomes $Z$ error on D5, and flips X4. Since X4 is not deterministic and it is the first time we measure it, how can we detect it?

Is there a way to think about it that does not demand going over all the possible two-qubit errors? Is there a way to see why all the black CNOT won't create any logical error without going over all of their errors one by one?

Answer 1

I thought about it quite a lot when reading the original paper by Li. Now, I think that I understood it, but please check carefully.

For example, regarding your question: IZ after the red gate (I always model all errors with an ideal gate and then the error) will cause a Z-error on D5, while doing nothing to X1 - so it is undetectable. Note, however, that you are doing the stabilizer measurement twice. So, in the first time you will get some result in X1, but on the second time IZ -> ZZ via the CNOT, so you will get a different result - and this is detectable.

On the contrary, ZZ will give you the same result twice: once because the Z error on the control, which is the ancilla, and the second time because of the propagation. So you will end up with with a logical error (Z on the magic qubit) which is undetectable.

Now, in general I don't know of a straight-forward way to see that without an exhaustive search. You can, however, make your life a little bit easier. One thing is that by trial and error you can get to some thumb-roles. For example, now that we understood the difference between ZZ and IZ (after the red CNOT), you immediately see that the reasoning of IZ do not hold for IX, because IX->IX through the CNOT, such that X1 will not detect it. Nevertheless, you need to be careful - how do I know that Z2 or Z3 will not detect it? Actually they will not, just because of the ordering that has chosen (the X will propagate once every round, so their measurement result will be the same).

Other way to make your life easier, maybe, is to use the Pauli web notation (see here and here, and it was also very recently done for the surface-code injection here). There, you will also need to check all options, but you can play with it diagrammatically so it might be easier.