Is entanglement distillation possible between states of different fidelities?

Question

I am looking for an algorithm that allows me to perform distillation from a pair of W-states of different fidelities. All the algorithms I found so far are focused on distilling identical states, which in practice may not be the case. Is there an algorithm that would give me the formula for the final state fidelity F, given the fidelities F1 and F2 of the input states?

Answer 1

In "Tetrationally Compact Entanglement Purification" I distill EPR pairs using a mix of low-error and high-error pairs. I feed high-noise EPR pairs into a low-noise EPR pair, which makes it better (I call it "boosting" in the paper but I think in the literature it's more commonly called "pumping"). However, boosting doesn't reach arbitrarily low error rates (even if you assume the postselected comparisons driving the distillation always succeed).

The issue is that, when you distill a high error rate pair against a low error rate pair (at least, the way I did it), the output inherits the high error rate along the basis of the comparison. So, for example, if you do an X basis comparison then the Y noise and Z noise will go down but the X noise will be at least as large as the high-noise state's noise. So you can only suppress errors in 2/3 of the Pauli bases using that technique. I fix the third basis having high error in a follow-up stage that streams the high-error-but-super-biased states that result from boosting into a following stage's low-error state, and use the biased noise to avoid the comparison basis' noise being high. But this can't reach error rates lower than the noise bias, eventually forcing another stage of boosting/pumping.

Any technique that could simply uncondtionally fold a high-error EPR pair into a low-error EPR pair to lowers its overall error rate would improve my result from requiring $O(\log^\ast(1/\epsilon))$ memory to requiring $O(1)$ memory to reach an error rate of $\epsilon$. So that'd be pretty cool.

---

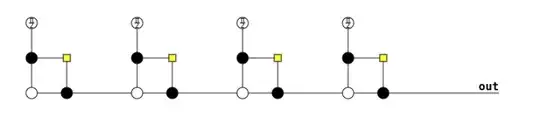
Interestingly, when distilling $|i\rangle$ states instead of EPR pairs, it is possible to just keep folding high-error states into a low-error state (assuming postselection keeps succeeding). I think this is because $|i\rangle$ is an eigenstate of Y, meaning it's immune to Y errors, so it's fine that there's a high noise basis when comparing states. Just make the noise basis the Y basis, and that noise becomes irrelevant due to the state being distilled. Here's a ZX graph of the streaming $|i\rangle$ distillation (where the $\pi/2$ should be interpreted as noisy, and everything else is perfect):

Just keep repeating that little widget to make the output arbitrarily good.