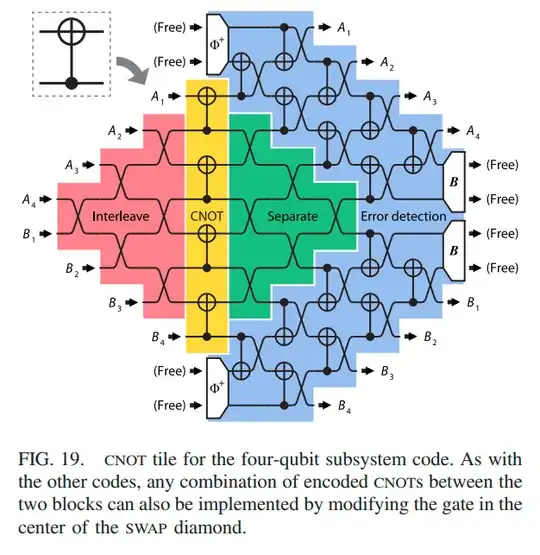
I have been under the impression that fault-tolerant universal quantum computation with nonvanishing thresholds requires at least two-dimensional connectivity of gates, not merely one-dimensional connectivity. However, this 1999 paper by Gottesman seems to challenge my belief.
Am I interpreting this correctly? If I lay out qubits on a line and I'm only allowed to perform faulty nearest-neighbor and next-nearest gates and local measurements of ancillas, can I perform universal quantum computation fault-tolerantly with a nonvanishing threshold?
I am still trying to understand the details of the construction.
In particular, I believe Gottesman argues that repeatedly concatenating a quantum error correcting code can nevertheless be done through local measurements of ancillas, many SWAP gates, and nearest-neighbor and next-nearest-neighbor gates along a line. To my understanding, the number of qubits are exponentially growing with the number of levels of concatenation, causing exponentially growing time delays when slowly shuffling qubits to measure stabilizer at a given level of concatenation. However, despite this, the recursive formulas for error rate at a given level of concatenation still give rise to a threshold.