1

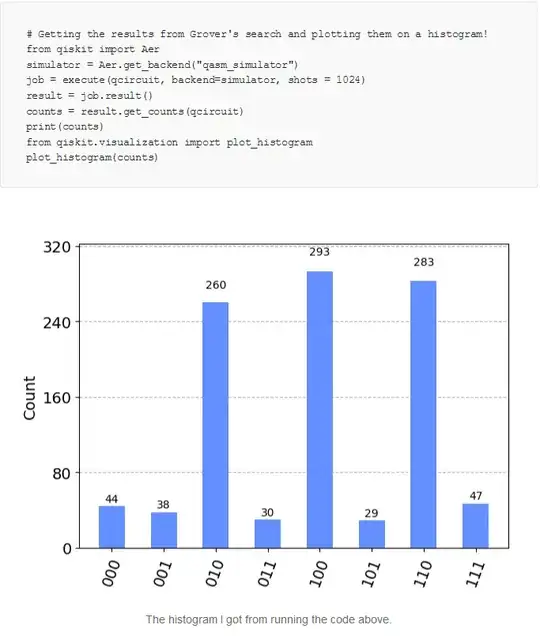
I'm working through a Qiskit tutorial on Grover search. Unfortunately it was published in 2023 and the tutorial's version of Qiskit (earlier than v1.00) is now out of date. I tried to rewrite the code in section "More Than One Marked Element" using Qiskit v1.0.2 with some success:

import numpy as np
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, transpile

our new "oracle"


def U(qc, q):
    num = ['010','100', '110']
    for i in num:
        Uf(i,qc,q)


defining a general Uf gate


def Uf(a,qc,q):
    for i in range(len(a)):
        if a[i]=='0':
            qc.x(q[len(a)-1-i])

    qc.mcx(control_qubits=list(range(0,q.size-1)), target_qubit=q[q.size-1])
    for i in range(len(a)):
        if a[i]=='0':
            qc.x(q[len(a)-1-i])


defining W


def W(qc,q):
    for i in range(q.size-1):
        qc.h(q[i])
        qc.x(q[i])
    qc.h(q[q.size-2])
    qc.mcx(control_qubits=list(range(0,q.size-2)), target_qubit=q[q.size-2])
    qc.h(q[q.size-2])
    for i in range(q.size-1):
        qc.x(q[i])
        qc.h(q[i])


n = 3  # no. qubits


create the quantum circuit


qreg1 = QuantumRegister(n+1)
creg1 = ClassicalRegister(n)
qcircuit = QuantumCircuit(qreg1,creg1)
qcircuit.x(qreg1[qreg1.size-1])  # initialize one state in ancillary qubit
qcircuit.h(qreg1)  # all qubits in superposition (changes ancillary to minus state)


iterations = np.pi/4np.sqrt(2*n)  # no. iterations


for i in range(round(iterations)):
    U(qcircuit, qreg1)
    qcircuit.barrier()
    W(qcircuit, qreg1)
    qcircuit.barrier()


qcircuit.measure(qreg1[0:qreg1.size-1],creg1)
qcircuit.draw(output="mpl")

Problems arise when I try to plot the histogram of results. The tutorial uses Qiskit's Aer and qasm_simulator functions which are deprecated:

code

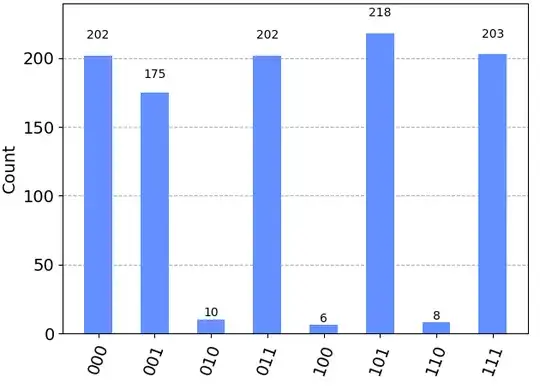
I attempted to rewrite this part, but my code does not produce the correct figure.

from qiskit_aer import QasmSimulator
simulator = QasmSimulator()
compiled_circuit = transpile(qcircuit, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
print(counts)
from qiskit.visualization import plot_histogram
plot_histogram(counts)

new

How do I fix this?

Medulla Oblongata
  • 287
  • 1
  • 9

1 Answers1

1

If you have $M$ marked element, then the number of iterations should be

$$\frac{\pi}{4}\sqrt{\frac{N}{M}} \text{where},\;\;\; N = 2^n $$

So, you need to replace this line

iterations = np.pi/4*np.sqrt(2**n)

with

iterations = np.pi/4*np.sqrt(2**n / 3)

Note also that, you should use floor() instead of round() to specify the number of iterations. Check out this answer for the details.

Egretta.Thula
  • 11,986
  • 1
  • 13
  • 34