I'm a novice at qutip simulation.
I was recently trying to use qutip to simulate the heating effect of a trapped ion by defining a jump operator defined with heating rate.
Below is the code of my simulation:
from qutip import *
from qutip_utils import *
exp_config = {
'lamb_dicke' : 0.095043,
'n_init' : 0.1,
'carrier_Rabi' : 2 * np.pi * 120 * 1000,
'dim' : 500,
'trap_freq' : 2 * np.pi * 1.02 * 1e6,
'init_T': 1e-5,
'gamma' : 1000} # no heating
max_N = exp_config['dim']
avg_n = exp_config['n_init']
ldf = exp_config['lamb_dicke']
rabi = exp_config['carrier_Rabi']
heating_rate = exp_config['gamma']
phonon_dm = thermal_dm(max_N, avg_n)
dstate = basis(2, 0)
ustate = basis(2, 1)
H0 = tensor(qeye(2), qeye(max_N))
rho0 = tensor(ket2dm(dstate), phonon_dm)
result = []
heating_time = 5e-3
times = np.linspace(0, heating_time, 100)
up_proj = tensor(ket2dm(ustate), qeye(max_N))
down_proj = tensor(ket2dm(dstate), qeye(max_N))
num_proj = tensor(qeye(2), create(max_N)*destroy(max_N))
jump_heat = np.sqrt(heating_rate)*tensor(qeye(2), create(max_N))
jump_ops = [jump_heat]
initial_state = rho0
H_heating = [H0]
motion_data = mesolve(H_heating, initial_state, times, jump_ops, num_proj, options={'store_states': True})
final_state_phonon = motion_data.states[-1].ptrace(1)
result.append(motion_data.expect[0][-1])
print(f'answer = {exp_config["gamma"] * heating_time}')
I have run the simulation where the heating lasts for heating_time = 5e-3 (5ms), which means the number of phonons increased should be approximately heating_rate times heating time ~= 5. However, If I run the simulation and get the expectation value of phonons after the heating (motion_data.expect[0][-1] part), I get 155.
Below is the gif that shows the change of phonon probability distribution of above simulation:
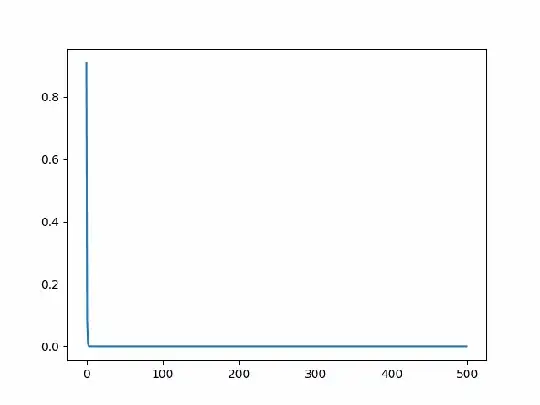
where Y axis is the probability value and X axis is the harmonic state (n) of phonon up to dim=500. At the very last of the simulation, there is an instantaneous spike at n~= 500, which seems wrong.
Is there anything I did wrong with my code? I assume modifying the defined hamiltonian could be one way of fixing this anomaly, but I'm not sure. Please help :(