Minimum number of CNOTs for Toffoli with non-adjacent controls

Question

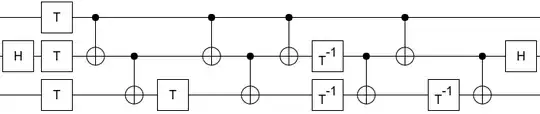
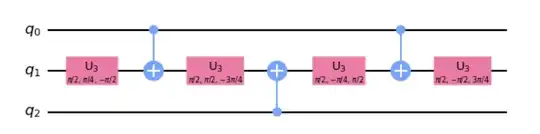
I want to decompose a Toffoli gate into CNOTs and arbitrary single-qubit gates. I want to minimize the number of CNOTs. I have a locality constraint: because the Toffoli is occurring in a linear array, the two controls are not adjacent to each other (so no CNOTs directly between the controls).

What is the minimum number of CNOTs required to perform this task? What is an example of a circuit which achieves this minimum?

To be specific, this is the layout I have in mind:

1 ---@---
     |
2 ---X---
     |
3 ---@---

Each control is adjacent to the target, but the controls are not adjacent to each other.

Answer 1

Here is the best construction I've found. It uses 8 CNOTs.

I verified this circuit in Quirk using the channel-state duality and a known-good inverse.

The target is the middle qubit. None of the CNOTs go directly from top to bottom or bottom to top. You can switch which qubit is the the target by simply switching which line the Hadamards are on.

Answer 2

I found this circuit with T-depth 3 using CPFlow (shameless plug).

Non-clifford gates (with T-count 1) are $R_Z(\pi/4)$ and $R_X(\pi/4)$. While most of the single-qubit non-Clifford gates in this circuit can probably be removed, circuits with shorter T-depth, T-count or CZ-depth are unlikely to be possible.

Community edit:

• This circuit in quirk
• Simplified variant using Control(Pauli,Pauli) interactions (ejected single qubit Cliffords)
• Simplified variant using CNOTs
• Simplified variant using CZs (folded single qubit gates)

Answer 3

I believe I've got it down to 9 controlled-not gates:

What I did was I used a set of three cNots in the place of Swap to move the two controls next to each other to achieve the last part of the standard Toffoli circuit (see here). This used 12 cNots.

However, the final $T$ and $H$ gates on the target qubit I propagated through one of these swaps. This let me cancel two controlled-Nots.

Then, in the final SWAP, I chose the first of the controlled-nots to be controlled from the middle qubit. I replaced it with a controlled-phase and two Hadamards. The leading Hadamard cancelled. The controlled-phase gate commutes with the preceding controlled gates controlled off the middle qubit, and phase gates on the middle qubit and bottom qubits. These operations bring that controlled phase up to a controlled-not from the first inserted swap. Hence, we can combine these two gates as a controlled-$iY$, controlled off the bottom qubit. But this can be written as a single cNot with some $S$ gates.

I've made no attempt at an optimality proof, but I'm already pretty pleased to have got it this small.

Answer 4

If you allow for a relative phase you can get your circuit to 3 $CNOT$s and 4 $U$ gates.