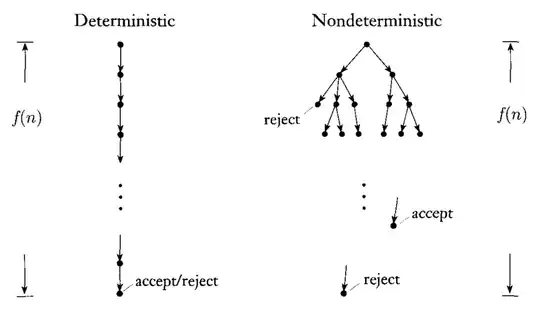
I am reading Niel de Beaudrap's answer in quantumcomputing.SE post to understand the workings of:
- Deterministic Turing Machine (DTM),
- Non-deterministic Turing Machine (NDTM) and
- Quantum Truing machine (QTM).
The transition tree model of these machines gives me a good insight into why NDTM easily simulates DTM.
[[ Image source: cs.se post ]]
My understanding: In the case of QTM,
I understand there exist some scenarios in which most of the transition paths get cancelled out (destructive interference) in such a way that the majority of the remaining paths end in an accepting state.
The probability of the QTM ending up on one of these surviving branches happens with the probability given by the amplitude associated with the transition path.
I understand BQP (or even BPP) is defined in terms of acceptance gap (say, BQP[2/3, 1/3]) (see second last paragraph of Neil's answer)
...A different approach to describing complexity classes is to consider instead the gap between the number of accepting branches and the number of rejecting branches of an NTM...
I could understand the above argument. It is the same reason why it is even unknown how to efficiently simulate a probabilistic Turing machine using NTM. That's why the relation between BPP and NP is still open.
But what if we included a probabilistic generalization of NTM? Or the machine that produces the certificate for the MA complexity class.
This 'MA machine' is known to (efficiently) simulate the BPP machine.
My query: What stops the MA machine (probabilistic NTM) from efficiently simulating QTM (BQP)?
Note:
I am aware of the fact that it is unlikely that BQP is contained in MA (due to a known (quantum) oracle separation between them).
I am just trying to build an intuition of the difficulty of efficiently simulating the QTM using probabilistic NTM. Preferably with the transition/computation tree model.