What Hilbert space of dimension greater than 4.3e19 would be most convenient for working with the Rubik's Cube verse one qudit? The cardinality of the Rubik's Cube group is given by: $$ |G|=43{,}252{,}003{,}274{,}489{,}856{,}000=2^{27}\cdot3^{14}\cdot5^3\cdot7^2\cdot11 $$
Examples.
This question does not need to be phrased as a quantum question. One can equally ask what classical register can be used to store a string that uniquely identifies each different configuration of the Rubik’s Cube. This is already implicitly answered in the question: you need 27 bits, 14 trits....
However, this is labouring under the assumption that you can easily pick and choose your information carrier, and combine together arbitrary sets with different dimensions, and easily talk about the logic operations on them and how they all interact. This is clearly not how it works in classical: your computer only processes bits (and if you want different dimensional systems, the software can handle the conversion: see, for example, the MixedRadix function in Mathematica), and the same will be true of quantum. A particular experiment will focus on one type of information carrier, and will be able to manipulate a certain number of levels. You might be able to repeat that many times, but you won’t be combining qubits, qutrits etc. So you’ll probably be using qubits, and you just need to find the smallest Hilbert space that’s larger than the required dimension. Again, as indicated by the question, that’s 66 qubits.
Perhaps the concern is that 66 seems like a lot of qubits and we need to make that number as small as possible. Remember that computations will require error correction, which means increasing the number of qubits by several orders of magnitude. One extra qubit doesn’t matter so much on the scale of things.
Following up on @DaftWullie's answer, for certain combinatorial puzzles such as the 3x3 Rubik's cube, it might also be convenient to consider a fixed register of qubits (or qubits and qutrits) for each cell of the cube, because then twists/turns of the faces almost immediately present themselves as (controlled) $\mathsf{SWAP}$'s of the respective cells.
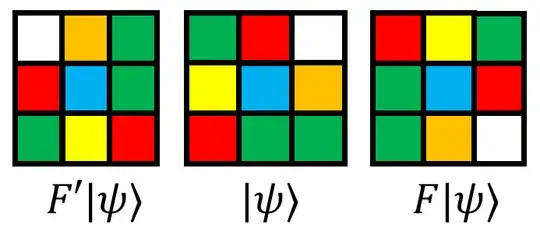
For example, consider the $9$ cells of the front face of a cube. Each cell (apart from the fixed center cell might correspond to $3$ qubits (or $1$ qubit and $1$ qutrit), with a fixed but arbitrary mapping of colors to qubits/qutrits, such as $f(\vert 000\rangle)\mapsto \text{BLUE}, f(\vert 001\rangle)\mapsto\text{RED}$, etc. The quarter-turn twists $F$ and $F'$ are simple permutations of the qubits, and $\vert\psi\rangle$ is the tensor product over each register.
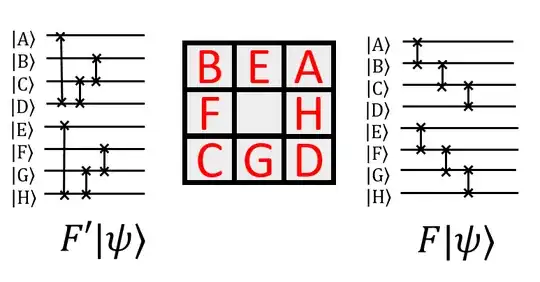
With such a set-up, the circuits that implement the permutations may be as above. Here, $\text{A,B,}\cdots$ are fixed registers of qubits (qutrits) of the cells on the front face, $F$ is a clockwise quarter-turn of the front face, and $F'$ is a counter-clockwise quarter turn. (The corner and cells adjacent to the front would also be permuted in a similar fashion).
I'm working out the circuits for a toy 2x2 version of the 15 puzzle, and another one for the Pyraminx. These have the advantage in that the number of colors/states is $4$, which means no qutrits would be needed. Indeed, the 2x2 puzzle is small enough that it could probably be implemented with existing hardware.
