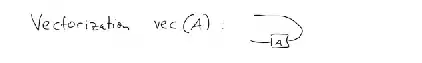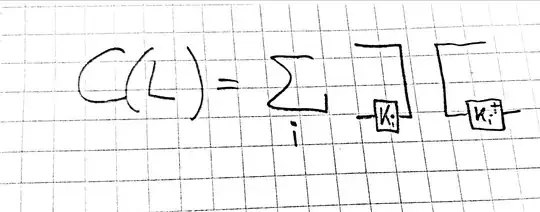I've been reading the following lecture notes in which two isomorphisms are defined:
- vectorization: $\text{vec}:B(H_A,H_B)\to H_A\otimes H_B$ and
- the Choi-Jamiołkowski isomorphism: $C:B(B(H_A), B(H_B )) \to B(H_A \otimes H_B )$ where $H_A, H_B$ are Hilbert spaces and $B(H)$ is the space of bounded linear operators on the Hilbert space $H.$
The graphical representation for $\text{vec}(A)$ is drawn on page 4, and reproduced here for convenience:
I think I understand it, but I'm struggling to draw a similarly intuitive picture of $C(L)$ for $L\in B(B(H_A), B(H_B))$
I'm aware that they are effectively equivalent, but I'd like to draw a diagram that would let me see immediately e.g. the identity listed as Lemma 1.3: $C(L) = (id_A\otimes L) (\omega_{d_A})$ (for $\omega_{d_A}$ the density matrix describing the $d_A$ dimensional maximally entangled state, or generalized Bell state) as well as similar such calculations.
Put simply, if $\text{vec}(A)$ is given by the picture above, what is $C(L)?$