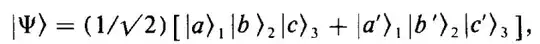TL;DR: No, these are not GHZ states. They are cat states.
GHZ state
The GHZ state is defined as the state
\begin{equation}
\frac{|000\rangle+|111\rangle}{\sqrt{2}}.\tag1
\end{equation}
Generalized GHZ state
More generally, the $n$-qubit state
\begin{equation}
\frac{|0^{\otimes n}\rangle+|1^{\otimes n}\rangle}{\sqrt{2}}\tag2
\end{equation}
is referred to as the generalized GHZ state. In both cases all qubits have equal labels.
That said, note that the label assignment to computational basis states (and indeed to any basis states) is a matter of convention. Still, for any choice of computational basis on $n$ qubits there exists a single GHZ state.
Cat states
A more general class of states, which includes the states where different qubits have potentially unequal labels, are the cat states. These are states of the form
\begin{equation}
\frac{|b\rangle+|\overline{b}\rangle}{\sqrt{2}}\tag3
\end{equation}
where $b\in\{0,1\}^n$ is a string of $n$ bits and $\overline{b}$ is the bit string obtained by flipping every bit in $b$.
In some areas, e.g. quantum optics, this term is used even more generally to refer to any state of the form $(|\psi\rangle+|\phi\rangle)/\sqrt{2}$ where $|\psi\rangle$ and $|\phi\rangle$ have small, but non-zero overlap $\langle\psi|\phi\rangle$. In such contexts, people often refer to the state with $\langle\psi|\phi\rangle=0$ as the "ideal cat state".