I may be wrong about this but when you run the QPE on some state $|\psi\rangle$ by simulating some Hamiltonian $H$, your precision is limited at least by:
- The error in the simulation of $U=\exp(-iHt)$;
- The precision you decide to choose for the phase estimation with the (inverse) Fourier transform; and
- The number of times you have to sample from the QPE using multiple copies of $|\psi\rangle$.
You can increase the precision with the first factor by using a larger Trotter factor or using more sophisticated Hamiltonian simulation. You can increase the precision of the second by adding an additional qubit of precision but you're still limited by the No Fast-Forwarding Theorem and you'd need to run your circuit for twice as long for each qubit of precision:
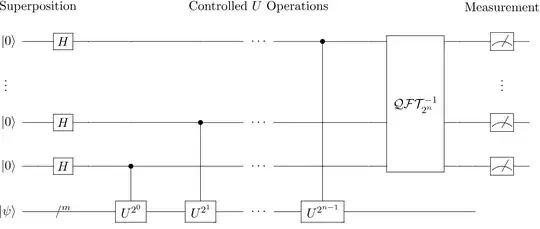
As for the third factor, if we are promised that $|\psi\rangle$ is an eigenstate then we only need to run the circuit once, because we'll get the phase right away. If $|\psi\rangle$ is in a superposition of two or more eigenstates and we don't know how much each contributes to $|\psi\rangle$, then I think you're right that statistics tells us the number of times we need to call the QPE grows quadratically.
But I think it's somewhat similar to a classical test. If we are given an audio signal that we are promised is a pure tone, and we have magical Born-rule box that will let us sample from the signal to return its frequency, it only takes one sample for us to know what the tone is. If we are given a signal that's a sum of two or more tones and we don't know the weight of each pure tone with respect to our signal, then I'm still pretty sure we'd have to run our Born box for a quadratic number of times to get a good estimte of $E_\psi$.
