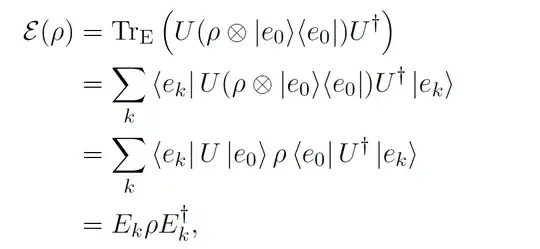I am having lot of trouble trying to understand the operator sum representation in Nielsen and Chuang:
I get the very first equation in above but how does that translate to 2 and how does the 3rd follow from the 2nd? Could someone please explain it to me? The only thing that we know from definition of partial trace is that:
The second line is the definition of a partial trace in Dirac notation (see here: https://physics.stackexchange.com/questions/179671/how-to-take-partial-trace). Like a standard trace, you sum over the diagonal elements with respect to the chosen basis (here is $|e_{k}\rangle$, which, for a 2 X 2 density matrix can be e.g. $|e_{0}\rangle = |0\rangle$ and $|e_{1}\rangle = |1\rangle$).
In the third line, notice that you begin from $\rho_{system} \otimes \rho_{env}$, where $\rho_{env} = |e_{0}\rangle\langle e_{0}|$. As such, the density matrix of the system $\rho$ acts on a completely different sub-space, so you can move $|e_{0}\rangle$ to the left over $\rho$.
The above answer by David Dentelski is comprehensive but I wanted to also offer some further information:
First to clarify exactly what the first line is saying, $\mathcal{E}(\rho)$ is a density matrix defined over some space Q equal to the outcome of the quantum operation $\mathcal{E}$ acting on an initial density matrix $\rho$, also defined on the space Q. The catch is $\mathcal{E}$ may also involve some interaction with the environment, which we call the space E. We can define this interaction to be the unitary operator U which acts on the joint space EQ. In the most general case, the environment can be assumed to initially be in some pure state which we call $|e_0 \rangle$ (see "purification of density operators"), then the resulting state in EQ after the unitary interaction will be the state $U(\rho ⊗ |e_0 \rangle \langle e_0|)$. However, in order to obtain $\mathcal{E}(\rho)$, which is only defined over the space Q, the final step is to trace over the possible outcomes of the environment.
In the second line, the {$|e_k \rangle$} basis is any orthonormal basis that spans the environment space E. There also will exist some basis for the space Q, where the density operator $\rho$ is defined, but { $|e_k \rangle$} does not extend to this space, and as such the trace is only carried out over the possible states of the environment leaving Q untouched. Physically this is motivated by our model assuming that we do not have any way to measure what state the environment ends up in (it would be nice if we did have a way because then we can say exactly which $E_i$ occurred!). So rather than treating the possible outcomes for $\rho$ as some set of {$\rho_i$} corresponding to each {$|e_i \rangle$} that the environment could end up in, we can instead obtain just one mixed state by summing over {$|e_i \rangle$}.
The third line isn't really saying anything different to the second line. It is just notationally more convenient to express the trace in terms of the objects $\langle e_k|U|e_0 \rangle$ and $\langle e_0|U^{\dagger}|e_k \rangle$, defined to be the operators $E_k$ and $E_k^{\dagger}$ respectively, as then the operator sum representation falls right out in the fourth line. Note that although the object $\langle e_k|U|e_0 \rangle$ looks like some inner product that should be a complex number, it isn't because {$|e_k \rangle$} is not a basis for EQ, or even a valid state in EQ, as the corresponding state for Q is not specified. $E_k$ is actually an operator that acts only on the space Q. As such our final expression for $\mathcal{E}(\rho)$ has no mention of the environment at all; indeed in many cases it can be interpreted without the existence of an environment in the first place, although it would be mathematically equivalent to the outcome that would be obtained if there were one.
Edit:
To answer specifically the question on how one can get from the 2nd to the 3rd line, if you really don't like the 3rd line you could just scrap it altogether and just go straight to the 4th line because it's not saying anything at all different to the 2nd. One conceptual way of seeing what's going on is if Q is a d-dimensional Hilbert space and E is a D-dimensional Hilbert space, imagine $U$ is expressed as some D-dimensional matrix of matrices, where each of the D$^2$ smaller matrices making up $U$ is itself d-dimensional. The result is one big dD-dimensional matrix representing the unitary transform $U$ on the joint space EQ, where each of the d-dimensional smaller matrices will then form the $E_k$ operation elements acting on Q. To obtain these operators, we simply take the inner product $\langle e_k|U|e_0 \rangle$ to 'pull out' the corresponding matrix element $U_{k0}$ which itself is a matrix equal to the corresponding operation element $E_k$ that will act on Q.
Note in this model the $U_{ki}$ elements corresponding to $i≠0$ are free to be whatever we want them to be such that $U$ is a unitary operator, because assuming the environment starts as $|e_0 \rangle$, the action of $U$ on other possible states of E is never seen. Of course for the case where $U$ is some real interaction on EQ and we obtain an operator-sum representation from there (rather than the other way around where one might want to construct $U$ given an operator sum representation on Q), we obviously won't have this freedom but nonetheless all of the above logic applies.
