How are stabilizers defined with monomial labellings for Bivariate Bicycle codes?

Question

I have been recently looking at getting familiarized with Bivariate Bicycle (BB) codes [1], and in general, Multivariate Bicycle codes [2]. I need some help figuring out the usage of the monomial labels for Pauli operator definitions.

---

Preliminaries (feel free to skip if you are familiar with the papers):

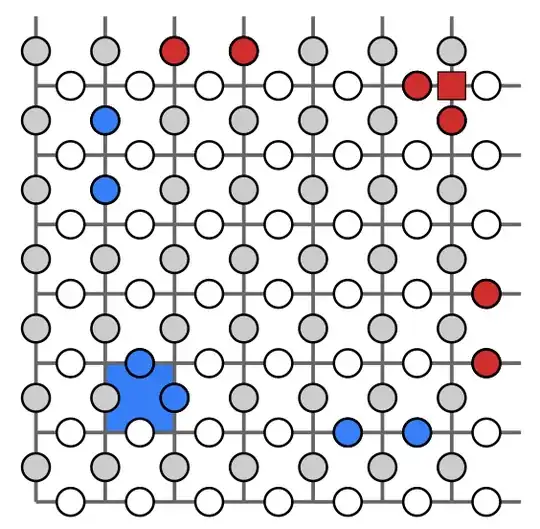
These families of QEC codes are defined via parity check matrices containing a two block structure of the form $H_{X} = (A|B)$ and $H_{Z} = (B^{T}|A^{T})$. The matrices $A$ and $B$ are both defined as polynomials of the form e.g. $A = x^3 + y^2 + y$, where each variable corresponds to a square matrix. In [1], these variables are defined as $x = S_{l} \otimes \mathbf{I}_{m}$ and $y = \mathbf{I}_{l} \otimes S_{m}$, where $S_{k}$ are cyclic matrices, meaning both $x$ and $y$ have dimensions ($lm$ x $lm$). As a result, counting the number of columns in $H_{X,Z}$, we obtain there are a total of $n=2lm$ data qubits.

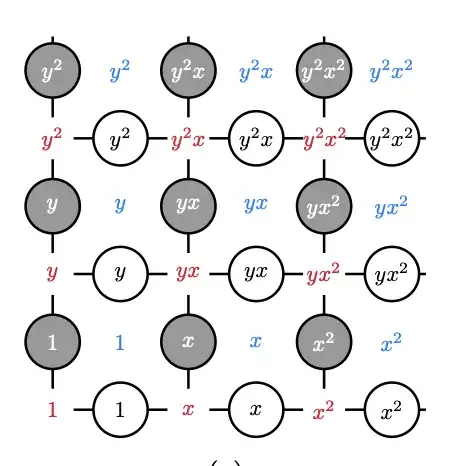
The two block structure of the parity check matrices is used to split data qubits into two registers "left" ($L$) and "right" ($R$). On the other hand, the checks are naturally split into $X$ and $Z$ depending on the type of stabilizer they are associated with. Each one of these four registers contains a total of $n/2=lm$ qubits (or nodes in the Tanner graph if you may). Naively, these qubits could be labelled by the set of integers $\mathbb{Z}_{lm} = \{0,1,\dots,lm-1 \}$. In [1,2], however, they instead use a monomial labelling, where each qubit is associated with an element from the set ${M} = \{1,y,\dots,y^{m-1},x,\dots,xy^{m-1},\dots,x^{l-1}y^{m-1} \}$. The integer set $\mathbb{Z}_{lm}$ can be easily mapped onto $M$ through $i \longrightarrow x^{\lfloor i/m \rfloor} \ y^{i-m\lfloor i/m \rfloor}$. Qubits in the system are then denoted as $q(T,\alpha)$, with $T\in \{ L,R,X,Z \}$ and $\alpha \in M$.

It is then possible to define Pauli operators by introducing the set of polynomials $\mathbb{F}_{2}^{M} = \{ \sum_{\alpha} p_{\alpha} \alpha : p_{\alpha} \in \ \mathbb{F}_{2} , \ \alpha \in M \}$. In particular, given $P,Q \in \mathbb{F}_{2}^{M}$, one denotes $X(P,Q)$ a Pauli qubit operator that acts as $X$ on all qubits $q(L,\beta)$ satisfying $\beta \in P$ and all qubits $q(R,\beta)$ satisfying $\beta \in Q$, and which acts as identity elsewhere. Same definition follows for $Z$.

---

Question

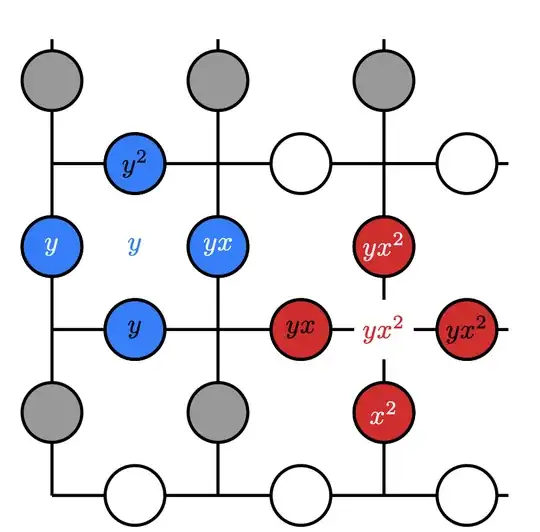
Using the notation above, in [1], it is said that an $X$ check labelled by $\alpha$, i.e. $q(X,\alpha)$, is connected to qubits $q(L,\beta)$ if $\beta \in A\alpha$ and to qubits $q(R,\beta)$ if $\beta \in B\alpha$. Therefore a generic $X$ stabilizer can be defined as $X(\alpha A, \alpha B)$. How should I understand the "multiplication" between the monomial $\alpha$ and the matrices $A,B$?

In [1], they state not to confuse this operation with vector multiplication, and emphasize that this corresponds to "multiplication of monomials" (for the case when one multiplies $\alpha$ with one of the terms $A_{i}(B_{i})$ in the definition of $A(B)$). However, how can this operation be well defined if $\alpha$ is a monomial belonging to $M$ whereas $A,B$ are square matrices? What is the correct interpretation?

Bonus question: Why is the monomial labelling for qubits interesting at all? How does this mathematical structure emerge naturally in this context?

Refs:

• [1] https://www.nature.com/articles/s41586-024-07107-7#Sec10
• [2] https://arxiv.org/pdf/2406.19151

Answer 1

Bivariate bicycle codes (BB codes) can be thought of as codes where the physical qubits sit on the edges of a 2D lattice. The integers $l$ and $m$ are the horizontal and vertical size of the lattice.

Inspired by the toric code, let's use the convention that each plaquette is a $Z$ type stabiliser and each vertex is an $X$ type stabiliser.

For example, for $l = m = 7$ it could look like this (because I just took a screenshot there are already some stabilisers in there, let's concentrate on the lattice as such):

Like this, we immediately verify that there are $l \cdot m$ $X$ type stabilisers, $l \cdot m$ $Z$ type stabilisers as well as $2\cdot l\cdot m$ physical qubits.

In fact, these physical qubits can be split into two ''sub-lattices'' of horizontal (white) and vertical (grey) qubits (qubits sitting on horizontal edges resp. vertical edges). Both of course have size $l\cdot m$ each.

Now, we can do something nice. We can label in each of the two sub-lattices the qubits, as well as each the $X$-type and the $Z$-type stabilisers, with monomials from $\mathbb{F}_2[x,y]/(x^l -1, y^m - 1)$ like this (in a smaller lattice now):

So basically the $x$-degree of the monomial tells you how far right you are, the $y$-degree how high up. The fact that we calculate modulo $(x^l -1, y^m - 1)$ nicely reflects that we have periodic boundary conditions here: If you are ''at the top'' (at height $m-1$) and go one step up, you come out at hight 0.

Then we can define our stabilisers such that

• the $Z$-type stabiliser labelled by a monomial $p$ checks all vertical qubits that appear as monomial terms in $A(x,y)p$ and all horizontal qubits that appear as monomial terms in $B(x,y)p$,
• and the $X$-type stabiliser labelled by a monomial $p$ checks all horizontal qubits that appear as monomial terms in $A(x^{-1},y^{-1})p$ and all vertical qubits that appear as monomial terms in $B(x^{-1},y^{-1})p$.

Note how we ''flipped everything'' going from $Z$ type stabilisers to $X$ type stabilisers: We exchanged ''horizontal'' with ''vertical'' and by using $A(x^{-1},y^{-1})$ instead of $A(x,y)$ resp. $B(x^{-1},y^{-1})$ instead of $B(x,y)$, we changed from going right with $x$ and up with $y$ to going left with $x$ and down with $y$.

So for the toric code, so $A(x,y) = 1 + x$ and $B(x,y) = 1 + y$, that looks like this:

As an exercise, one can label the qubits and checks in the first screenshot above and figure out what $A(x,y)$ and $B(x,y)$ are here, a solution to the exercise is in the caption of Figure 1 in 3 :)

So I think this is a very nice way of thinking about the BB codes and thinking about them in terms of polynomials rather that induced by the parity check matrices that arise by inputing these permutation matrices into the polynomials yields nice structural insights.

All screenshots are from 3.

3 https://arxiv.org/pdf/2407.03973