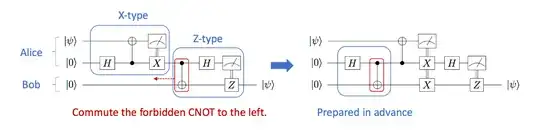
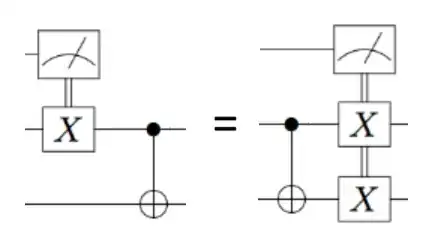
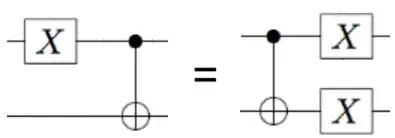
I am doing some Quantum Computing Exercises and I am curious on how you go from left to right in this picture...
I see not only how the c-not moves but also a new bond between X gates in second and third qubit..
I have been trying to find the equalities used but it's hard... does someone know the step by step on how to go from the left circuit to the right?
Basically, all we need to prove is the following identity:
Then the CNOT we have just moved past the feed-forward operation commutes trivially with the other CNOT to its left, since they just have one control-qubit in common.
The simplest way to prove the circuit identity shown in the diagram above is to consider the two possible measurement outcomes separately. If the top qubit is measured in $|0\rangle$, then we end up with just the CNOT on the two remaining qubits, as none of the operations conditional on the measurement outcome is triggered. If instead the top qubit is measured in $|1\rangle$, we obtain the following circuit identity:
It can easily be checked that this identity is true.
You have the state $UC|\psi\rangle$ but are more interested in obtaining an expression like $\tilde{C}U|\psi\rangle$, where the $\tilde{C}$ has changed accordingly. The way to do this is rewrite $$UC|\psi\rangle = UCU^\dagger U|\psi\rangle = \tilde{C}U|\psi\rangle$$ Where $\tilde{C} = UCU^\dagger $. Computing this term and writing it as a product of standard circuit gates would tell you how other gates are affected when you pass it through the circuit.
you can check the ZX calculus, it has simple rules that will allow you to prove this in a far easier road, and aid you to find equivalent circuits in a really simple way. In fact, the most famous example in ZX is the teleportation protcol circuit being extracted purely from one line going from A to B! One year since i discovered it and it is still surprising me with how robust it is! ref: https://zxcalculus.com/
