Incorrectly Calculating Probability Amplitudes for 3-qbit Circuit

Question

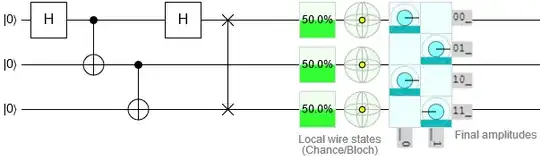
I’m trying to calculate the probability amplitudes for this circuit:

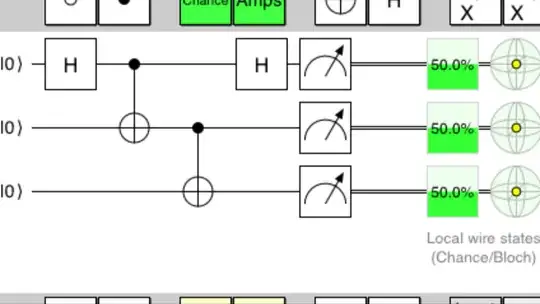
My Octave code is:

sys = kron([1; 0], [1;0], [1;0])
h = 1/sqrt(2) * [1 1; 1 -1];
c = [1 0 0 0; 0 1 0 0; 0 0 0 1; 0 0 1 0];
op1 = kron(h, eye(2), eye(2));
op2 = kron(c, eye(2));
op3 = kron(eye(2), c);
op4 = kron(h, eye(2), eye(2));
op4*op3*op2*op1 * sys

The output is:

ans =
0.50000
0.00000
0.00000
0.50000
0.50000
0.00000
0.00000
-0.50000

This differs from the results the quantum circuit simulator gives me, where have I gone wrong?

Answer 1

You're getting the same output as Quirk, just with a different bit ordering convention for the kets.

Quirk considers the top qubit to be the "least significant" qubit (i.e. if you count 000, 001, 010, ... then it refers to the rightmost bit). So if you apply a Hadamard gate to the top qubit of a three-qubit circuit in Quirk you get the state |000> + |001>.

In your code you are using the opposite convention, and putting the H as the first argument to kron instead of the last argument, so you would get |000> + |100> instead.

To get comparable results you just need to vertically mirror the Quirk circuit, e.g. by throwing in a swap gate:

Answer 2

The output you've stated there appears to be correct. The Hadamard produces $$ |000\rangle\mapsto\frac{1}{\sqrt{2}}(|000\rangle+|100\rangle). $$ Then, the two controlled-nots give $$ \mapsto\frac{1}{\sqrt{2}}(|000\rangle+|111\rangle). $$ The final Hadamard then yields $$ \mapsto\frac{1}{2}((|0\rangle+|1\rangle)|00\rangle+(|0\rangle-1|\rangle)|11\rangle). $$ This is the same as $\frac12(|000\rangle+|011\rangle+|100\rangle-|111\rangle)$.

The problem is presumably with the quantum simulator, or your interpretation of it, but since you don’t specify what simulator you’re using, it’s difficult to know...