Unital qubit channels as a convex combination of entanglement-breaking and unitary channel

Question

I am trying to show that for $T:B(\mathbb{C}^{2})\rightarrow B(\mathbb{C}^{2})$ a unital qubit channel, that T is a convex combination $T=pB+(1-p)Ad_{V}$, where B is a Entanglement-Breaking(EB) channel and $Ad_{V}(X)=VXV^{\dagger}$, for V unitary.

My idea is to use that all unital qubit channels can be expressed as $T(X)=Tr[X]\frac{\mathbb{1}}{2}+\frac{1}{2}\sum_{i} \lambda_{i}Tr[\sigma_{i}X]\sigma_{i}$, where $\sigma_{i}'s$ are the Paulis, and we also know that $Tr[X]\frac{\mathbb{1}}{2}$ is EB. The step where I'm unsure: I then say that $\frac{1}{2}\sum_{i} \lambda_{i}Tr[\sigma_{i}X]\sigma_{i}=Ad_{V}(X)$, since each $\lambda_{i}Tr[\sigma_{i}X]\sigma_{i}$ is just a transformation on the Bloch sphere?

Is this correct intuition, or is there another solution?

Answer 1

As I see it the only way to obtain the result in question is to first understand the geometry of diagonal Pauli channels, i.e. channels the Pauli transfer matrix of which is diagonal. For a map $\Phi$ with Pauli transfer matrix ${\rm diag}(1,a,b,c)$—so $\Phi$ is automatically trace-preserving and unital—the following three facts are important:

• $\Phi$ is positive if and only if $a,b,c\in[-1,1]$
• $\Phi$ is completely positive if and only if the Fujiwara-Algoet conditions (arXiv) $|a\pm b|\leq |1\pm c|$ hold. Equivalently, $(a,b,c)$ lies in the Fujiwara-Algoet tetrahedron which is defined as the convex hull of the points $(1,1,1)$ (represents identity channel), $(1,-1,-1)$ (represents Pauli-X), $(-1,1,-1)$ (represents Pauli-Y), and $(-1,-1,1)$ (represents Pauli-Z)
• $\Phi$ is completely positive and entanglement-breaking if and only if $|a|+|b|+|c|\leq 1$, cf. Theorem 4 in Ruskai's paper "Qubit Entanglement Breaking Channels" (arXiv) from 2003. Equivalently, $(a,b,c)$ lies in the convex hull of the points $(1,0,0)$, $(0,1,0)$, $(0,0,1)$, $(-1,0,0)$, $(0,-1,0)$, $(0,0,-1)$.

This lets us visualize things as follows:

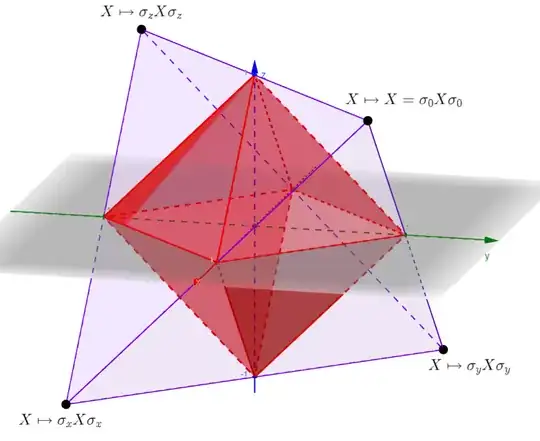
The purple tetrahedron is the set of all Pauli-diagonal channels, and the red diamond sitting inside is the set of all entanglement-breaking Pauli-diagonal channels. Note how the corners of the purple tetrahedron are precisely the Pauli channels (unitary!). This geometric insight will be the key to proving the following:

Theorem. Given any unital channel $T:\mathbb C^{2\times 2}\to\mathbb C^{2\times 2}$ there exist

• a Pauli-diagonal and entanglement-breaking channel $B:\mathbb C^{2\times 2}\to\mathbb C^{2\times 2}$
• $U_1,U_2\in\mathbb C^{2\times 2}$ unitary
• $p\in[0,1]$

such that $T=p({\rm Ad}_{U_1}\circ B\circ {\rm Ad}_{U_2})+(1-p)({\rm Ad}_{U_1}\circ {\rm Ad}_{\sigma_c} \circ{\rm Ad}_{U_2})$ for some $c\in\{0,x,y,z\}$. In particular every such $T$ is the convex combination of an entanglement-breaking unital channel and a unitary channel.

Proof. I will not flesh out every detail but I will give the idea for how to construct the desired decomposition. As I mentioned in my comment every unital qubit channel is similar to a Pauli-diagonal channel so there exist unitaries $U_1,U_2$ such that ${\rm Ad}_{U_1^\dagger}\circ T\circ {\rm Ad}_{U_2^\dagger}$ is Pauli diagonal. In particular this channel is characterized by some vector $\Phi:=(a_1,a_2,a_3)\in[-1,1]$ which satisfies Fujiwara-Algoet, i.e. $\Phi$ lies in the purple tetrahedron. Now there are two cases:

1. $\Phi$ lies in the red diamond, i.e. $T$ is already entanglement-breaking. Then we choose $p=1$ and $B=T$ and we are done.
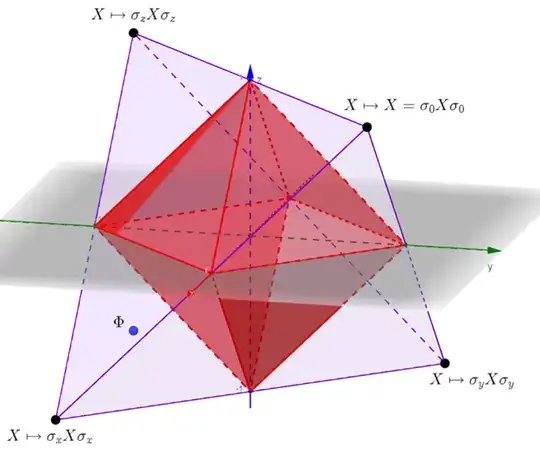
2. $\Phi$ does not lie in the red diamond. Choose the corner of the Fujiwara-Algoet tetrahedron that $\Phi$ is closest to; in this example image this would be the X-corner $(1,-1,-1)$:

Then draw the ray from this corner through $\Phi$; by construction it will intersect the red diamond in some point $b$:

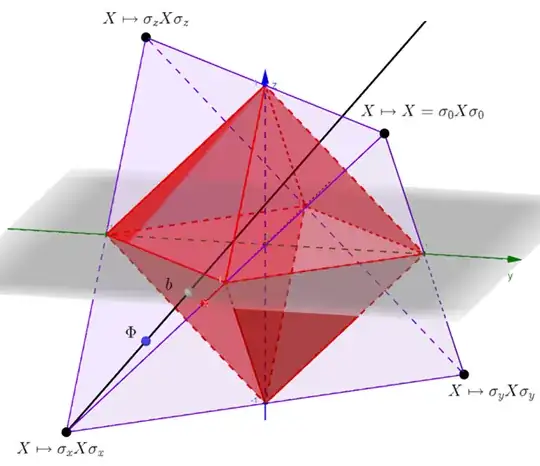
In particular, because $\Phi$ lies between the corner $c$ in question and $b$ there exists $p\in[0,1]$ such that $\Phi=pb+(1-p)c$. But this point $b$ corresponds to an entanglement-breaking Pauli-diagonal channel $B$ meaning the decomposition we found is equivalent to $$ {\rm Ad}_{U_1^\dagger}\circ T\circ {\rm Ad}_{U_2^\dagger}=pB+(1-p){\rm Ad}_{\sigma_c}\,. $$ Getting $U_1,U_2$ to the other side yields the desired decomposition $$ T=p{\rm Ad}_{U_1}\circ B\circ {\rm Ad}_{U_2}+(1-p){\rm Ad}_{U_1}\circ{\rm Ad}_{\sigma_c}\circ {\rm Ad}_{U_2}\,.\tag*{$\square$} $$