Are there even distance color codes?

Question

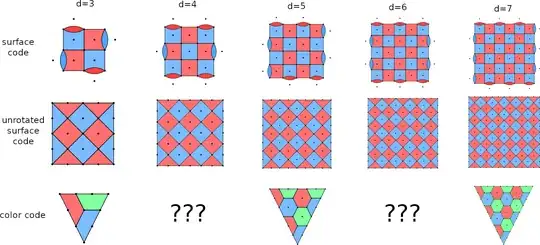
The surface code comes in both odd-distance and even-distance forms. Color codes always seem to come in odd-distance. Presumably this is due to the fact that the X and Z observables overlap at the boundary of a color code, and they must anticommute, forcing an odd boundary length. But is this actually a constraint, or are there ways to get nice even-distance color codes? What if implicit assumptions are dropped, like planar vs toric topology or the usage of two-color-type boundaries instead of pauli-type boundaries?

Answer 1

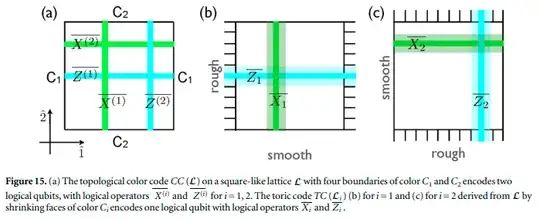
Color codes on a torus or with boundaries of two colors (as you suspected) that encode 4 and 2 logical qubits respectively can have even distance. For a general view on that, see for example

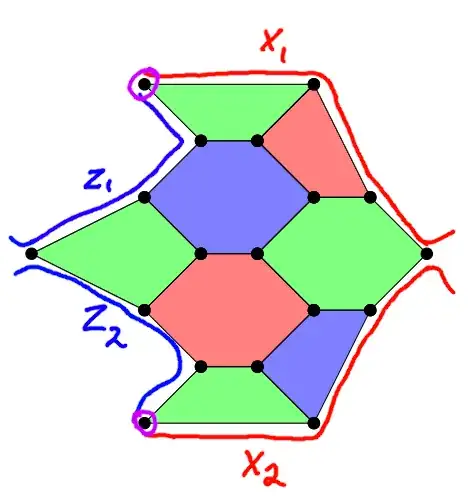
• "Unfolding the color code" Fig. 15 (https://iopscience.iop.org/article/10.1088/1367-2630/17/8/083026/pdf), or

  

• the boundary section of "The boundaries and twist defects of the color code and their applications to topological quantum computation" (https://quantum-journal.org/papers/q-2018-10-19-101/pdf/).

  

To my knowledge, there hasn't been done much work on concrete examples, but e.g.

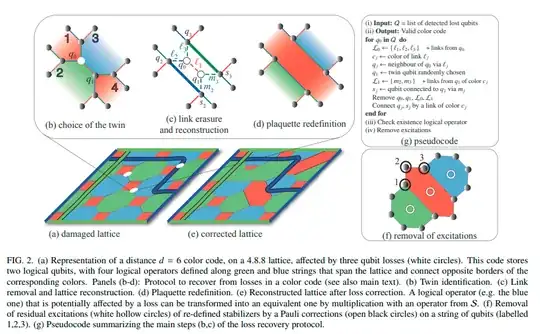
• Fig. 2 in "Twins Percolation for Qubit Losses in Topological Color Codes" (https://arxiv.org/abs/1802.04545),

  

shows a distance 6 planer color code.

Answer 2

I think toric color codes always have even distance, e.g.

from https://arxiv.org/abs/quant-ph/0703272.

Answer 3

This is more of a train of thoughts than a full answer, but I think it makes a case for the need to relax some assumptions.

You are probably aware of color codes layed on a torus that have an even distance. The question is then: can we find an even distance color code that encodes only one qubit?

In a typical color code, I would argue that any set of qubits that is the support of a $Z$ logical operator is also the support of an $X$ logical operator. Indeed, any $X$ stabilizer can be paired with a $Z$ stabilizer acting on the same qubits, so a $Z$ Pauli operator that commute with all the $X$ stabilizers will naturally be paired with a $X$ Pauli operator commuting with all the $Z$ stabilizers.

Moreover, either both or none of them are the product of some stabilizers thanks to the correspondence between stabilizers, so either both or none of them act non-trivially on the logical state. If the color code encodes only one logical qubit, then each non-trivial $Z$ (or $X$) logical operator must anticommute with its same support $X$ (or $Z$) counterpart. In particular, this is true for the logical operator with the lowest weight, so the distance of the code should be odd.

I am not familiar with more complex boundaries, but I think you would need to have some $Z$ stabilizers that are not paired with same support $X$ stabilizers to break the symmetry between logical operators.

I wonder if anything can be deduced from the unfoldability property of color codes...

Answer 4

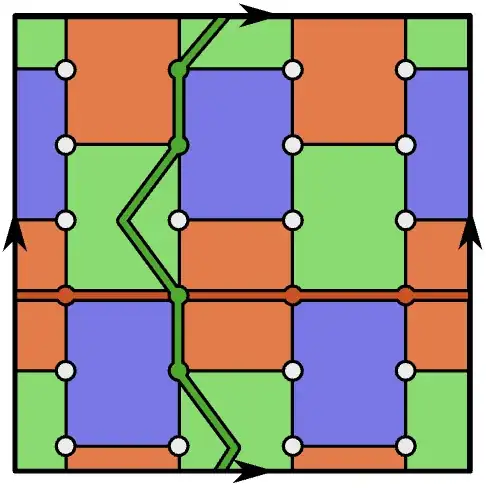
One way to get an even distance color code is by making a square patch that alternates between GB and RG boundaries on its sides. This has two logical qubits instead of one. For example, here is an [[18, 2, 4]] color code: