#!/usr/bin/env python
# coding: utf-8
In[1]:
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from qiskit_aer import AerSimulator, Aer
from qiskit.visualization import plot_histogram, plot_bloch_multivector, plot_distribution
from qiskit_ibm_runtime import QiskitRuntimeService
from numpy import pi
import numpy as np
import math
import matplotlib.pyplot as plt
from qiskit.circuit.library import ZGate, XGate, RZGate, SGate
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
from qiskit_ibm_runtime import Session, SamplerV2 as Sampler
service = QiskitRuntimeService()
In[2]:
def diffuser(nqubits):
#import pdb; pdb.set_trace()
circ = QuantumCircuit(nqubits)
# Apply transformation |s> -> |00..0> (H-gates)
for qubit in range(nqubits):
circ.h(qubit)
# Apply transformation |00..0> -> |11..1> (X-gates)
for qubit in range(nqubits):
circ.x(qubit)
# Do multi-controlled-Z gate
circ.h(nqubits-1)
circ.append(XGate().control(nqubits-1), list(range(nqubits)))
circ.h(nqubits-1)
# Apply transformation |11..1> -> |00..0>
for qubit in range(nqubits):
circ.x(qubit)
# Apply transformation |00..0> -> |s>
for qubit in range(nqubits):
circ.h(qubit)
# We will return the diffuser as a gate
U_s = circ.to_gate()
U_s.name = "U_0"
return U_s
In[3]:
apply inverse phase shift rotation gates in recursive
def inv_qft_rotation(circuit, n, m):
if n==0:
return circuit
# get theta index for rotation
l = range(2, m-n+2)
revl = list(l)[::-1]
control_idx = 0
n-=1
for k in revl:
circuit.cp(-pi/2**(k-1), control_idx, m-n-1)
control_idx+=1
circuit.h(m-n-1)
return inv_qft_rotation(circuit, n, m)
In[4]:
apply swap gates
def qft_swap(circuit, n):
# num of times of swap
swap_num = (int)(n/2)
m = n-1
for i in range(swap_num):
circuit.swap(i, m)
m -= 1
In[5]:
apply inverse qft transform
def inv_qft(circuit, n, m):
qft_swap(circuit, n)
inv_qft_rotation(circuit, n, m)
In[6]:
apply phase shift rotation gates in recursive
def qft_rotation(circuit, n):
if n==0:
return circuit
n-=1
circuit.h(n)
control_idx = n-1
for k in range(2, n+2):
circuit.cp(pi/2**(k-1), control_idx, n)
control_idx-=1
return qft_rotation(circuit, n)
In[7]:
apply swap gates
def qft_swap(circuit, n):
# num of times of swap
swap_num = (int)(n/2)
m = n-1
for i in range(swap_num):
circuit.swap(i, m)
m -= 1
In[8]:
apply qft transform
def qft(circuit, n):
qft_rotation(circuit, n)
qft_swap(circuit, n)
In[9]:
problem1
sudoku
---------
|V0 | V1|
|-------|
|V2 | V3|
---------
In[10]:
clause_list = [[0,1], [2,3], [0,2], [1,3]]
In[11]:
def XOR(qc, a, b, output):
qc.cx(a, output)
qc.cx(b, output)
In[12]:
nqubits = len(clause_list)
tqubits = nqubits + 1
In[13]:
prepare registers
count_qubits = QuantumRegister(tqubits, name='count')
var_qubits = QuantumRegister(nqubits, name='v')
clause_qubits = QuantumRegister(nqubits, name='c')
output_qubit = QuantumRegister(1, name='out')
meas = ClassicalRegister(tqubits, name="meas")
qc = QuantumCircuit(count_qubits, var_qubits, clause_qubits, output_qubit, meas)
#qc.draw()
In[14]:
apply QFT/hadamard gate
#qc.h(count_qubits)
qft(qc, tqubits)
qc.h(var_qubits)
#qc.barrier()
#qc.draw()
In[15]:
def sudoku_oracle(nqubits):
var_qubits = QuantumRegister(nqubits)
clause_qubits = QuantumRegister(nqubits)
output_qubit = QuantumRegister(1)
circ = QuantumCircuit(var_qubits, clause_qubits, output_qubit)
# Compute clauses
i = 0
#compute clauses
for clause in clause_list:
XOR(circ, var_qubits[clause[0]], var_qubits[clause[1]], clause_qubits[i])
i += 1
# inverse the output qubit if all the control bits are 1.
circ.append(XGate().control(nqubits), list(clause_qubits)+[output_qubit])
circ.z(output_qubit)
circ.append(XGate().control(nqubits), list(clause_qubits)+[output_qubit])
#uncompute clauses
i = 0
for clause in clause_list[::-1]:
XOR(circ, var_qubits[clause[1]], var_qubits[clause[0]], clause_qubits[nqubits-1-i])
i += 1
U_f = circ.to_gate()
U_f.label = "U_f"
return U_f
In[16]:
def get_grover_op(niter, nqubits):
#import pdb; pdb.set_trace()
var_qubits = QuantumRegister(nqubits)
clause_qubits = QuantumRegister(nqubits)
output_qubit = QuantumRegister(1)
q = QuantumCircuit(var_qubits, clause_qubits, output_qubit)
for i in range(niter):
q.append(sudoku_oracle(nqubits), list(var_qubits)+list(clause_qubits)+[output_qubit])
q.append(diffuser(nqubits), list(var_qubits))
U_g = q.to_gate()
U_g.label = f"Grover$^{niter}$"
return U_g
In[17]:
repetitions = 1
for counting_qubit in range(tqubits):
#import pdb; pdb.set_trace()
gop = get_grover_op(repetitions, nqubits)
circ_grover_iter = gop.control()
qc.append(circ_grover_iter, [count_qubits[counting_qubit]]+list(var_qubits)+list(clause_qubits)+[output_qubit])
repetitions *= 2
In[18]:
Apply inverse QFT
inv_qft(qc, tqubits, tqubits)
for i in range(tqubits):
qc.measure(count_qubits[i], meas[i])
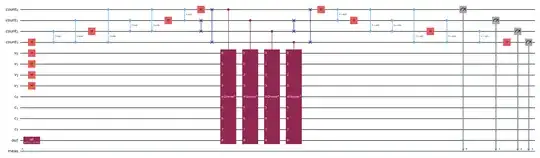
qc.draw("mpl",plot_barriers = False,fold=-1)
In[19]:
backend = AerSimulator()
pm = generate_preset_pass_manager(backend=backend, optimization_level=0)
shots = 1024
isa_qc = pm.run(qc)
sampler = Sampler(backend)
result = sampler.run([isa_qc], shots=shots).result()
pub_result = result[0]
counts = pub_result.data.meas.get_counts()
plot_distribution(counts, title="phase estimation")
In[20]:
measured_str = max(counts, key=counts.get)
measured_int = int(measured_str, 2)
print("Register Output = %i" % measured_int)
In[21]:
theta = pi * measured_int/(2**tqubits)
print("theta = %f" % theta)
In[22]:
N = 2nqubits
print("N = %i" % N)
M = N * (math.sin(theta)2)
print("num of solutions : %f " % (N-M))
In[ ]: